
前回までで見たように、ニューラルネットワーク (特に、畳み込みニューラルネットワーク) は多くの計算を必要とする。 そのため、ある程度の大きさの画像を対象とした 実用的なモデルを学習しようとすると、 既存のパソコンの性能では不十分な場合が出てくる。 そこで現在のディープラーニングでは、 GPU (Graphical Processing Unit) を利用することが多い。 GPU はもともと 3Dグラフィックスのための計算をおこなう装置だったが、 その基本は並列処理であり、現在ではグラフィックス以外の用途にも利用されている。 現在のところ、GPU を一般的な用途に利用する枠組みとしては NVIDIA の CUDA が ほぼデファクト・スタンダードである (類似のオープンな規格として OpenCL があるが、 2021年の時点ではまだマイナーな存在である)。
GPU は CPU に比べて単純な処理しかできないが、CPU に比べて はるかに多くの処理を並列実行できるため、ある種のアルゴリズムに対しては CPU に比べて数倍〜数十倍の速度が出せる。ニューラルネットワークで 行われる演算はほとんどが足し算と掛け算なので、 とくに GPU で処理するのに向いているといえる。 NVIDIA が提供する CUDA 開発キットには GPU 用のコードが 生成できるよう拡張された C/C++コンパイラ (nvcc) が付属している。 これを使った簡単な C プログラムの例を以下に示す:
#include <stdio.h> /* GPU で(並列に)実行される関数 */__global__ void mult(float* out, float* a, float* b, int n) { for (int i = 0; i < n; i++) { out[i] = a[i] * b[i]; } }int main(int argc, char* argv[]) { int n = 1000000; /* データを用意する。 */ float* a = (float*)malloc(sizeof(float) * n); float* b = (float*)malloc(sizeof(float) * n); float* out = (float*)malloc(sizeof(float) * n); for (int i = 0; i < n; i++) { a[i] = b[i] = i; } /* GPU上にデータ領域を割り当てる。 */ float* c_a; float* c_b; float* c_out; cudaMalloc(&c_a, sizeof(float) * n); cudaMalloc(&c_b, sizeof(float) * n); cudaMalloc(&c_out, sizeof(float) * n); /* CPU→GPU にデータを転送する。 */ cudaMemcpy(c_a, a, sizeof(float) * n, cudaMemcpyHostToDevice); cudaMemcpy(c_b, b, sizeof(float) * n, cudaMemcpyHostToDevice); /* GPU 上で関数を実行する。 */ mult<<<1, 1>>>(c_out, c_a, c_b, n); /* 計算結果を GPU→CPU に転送する。 */ cudaMemcpy(out, c_out, sizeof(float) * n, cudaMemcpyDeviceToHost); /* 計算結果を表示する。 */ printf("out[0]=%f\n", out[0]); printf("out[n-1]=%f\n", out[n-1]); /* 領域を開放。 */ cudaFree(c_a); cudaFree(c_b); cudaFree(c_out); free(a); free(b); free(out); return 0; }
上のコードのうち __global__ 宣言がある関数
mult
(CUDA ではカーネルと呼ばれるが、
これはもともと各ピクセルごとの演算をさせていた名残りだと思われる) が
GPU 上で走るバイナリにコンパイルされ、
mult<<<1, 1>>>(...);
という書式で呼び出される。プログラム中に「CPU-GPU 間のデータ転送」を
おこなっている部分があるのに注目してほしい。
GPU が動作する手順は以下のようになっている:
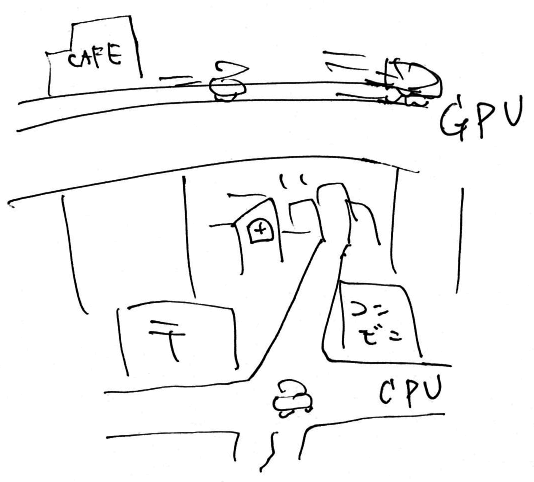
GPU は通常の CPU が使う主記憶とは独立したメモリを持っている。 GPU を使ううえで注意すべきことは、たとえ計算処理が高速であっても データ転送にはそれなりに時間がかかるということである。 CPU と GPU の関係は、一般道路と高速道路に似ている。 高速道路上では速く移動できるが、移動以外にできることは限られている。 とはいえ、乗り降りには時間がかかるため、一度高速道路に乗ったら、 なるべくそこから降りずに目的地の近くまで到達したい。 GPU におけるプログラミングも同様で「いかにCPU-GPU間の転送を少なくするか」が 効率のよいアルゴリズム設計の肝である。
Linux 上で CUDAをインストールし、 上のプログラムを実際にコンパイル・実行せよ:
$ nvcc mult.cu $ ./a.out
PyTorch はいわゆる「機械学習フレームワーク」と 呼ばれるソフトウェアの一種であり、効率のよいニューラルネットワークを 簡単に実装するために開発された。 PyTorch を使う利点は 3つある:
backward() メソッドを書く必要がない。
利点 1. の効率化もさることながら、
プログラマにとって特に大きなメリットは 2. である。
前章までのプログラムと同じく、PyTorch によるプログラムでも基本は
各レイヤーがどのように入力を処理するか (forward() メソッド) を
実装していくが、勾配が自動的に計算されるので、プログラマはそれ以外の
部分を考える必要がない。そして 3. の利点により、実際には多くの場合
既製のレイヤーを使うことで、 forward() すら書く必要がない。
したがって、PyTorch を使ったプログラムは計算手順というよりも
むしろ「各レイヤーをどのように結合するか」という記述に近い。
本章ではこれを使ってより高速かつ複雑なネットワークを作成し、
実用的な問題に応用していくことにしよう。
NumPy と同じく、torch モジュールも素の Python には含まれていないので、 インストールする必要がある。 ここではついでに画像を処理するモジュールである Pillow も インストールしておこう (Google Colab を使っている場合はどちらもインストール不要):
C:\> conda install -c pytorch pytorch C:\> conda install -c anaconda pillow
C:\> pip install torch -f https://download.pytorch.org/whl/torch_stable.html C:\> pip install pillow
Python 中で PyTorch モジュールを使うときは、
以下のように import する:
import torch
ただし、PyTorch のバージョン (あるいはハードウェアの構成) によっては GPU (CUDA) が使えない場合もある。GPU が利用可能かどうかは、 以下のようにして判定できる:
>>> import torch >>> torch.cuda.is_available() True
ニューラルネットワークの実装に入る前に、まず PyTorch における
重要なデータ型である Tensor (テンソル) 型について説明する。
本来、数学では「テンソル」はもうすこし抽象的な意味をもつが、
機械学習における「テンソル」は「多次元配列」とほぼ同義である。
したがって Tensor型の基本機能も NumPy における
ndarray型とほとんど同じであり、使い方もわざと
ndarray型に似せてある。
ただし、以下のような機能が追加されている:
Tensor上のデータは、CPU上の主記憶か、
あるいは GPU上のメモリのどちらに格納するか選ぶことができる。
Tensor上の各数値は、
それが計算されたときの勾配 (grad) を保持することができる。
Tensorを作成するには、以下の方法がある:
>>> torch.tensor([1,2,3,4]) # 4要素のPythonリストからTensorを作成 >>> torch.tensor([[1,2,3], [4,5,6]]) # 2×3要素のPythonリストからTensorを作成 >>> torch.zeros(4) # 4要素すべてゼロ >>> torch.zeros((2, 3)) # 2列3行すべてゼロ >>> torch.rand(4) # 4要素の乱数 (0〜1の範囲) >>> torch.rand((2, 3)) # 2列3行の乱数 (0〜1の範囲)
Tensor型に変換せよ。
torch.rand((3, 3)) の値を表示せよ。
畳み込みネットワークでは、各レイヤーへの画像の入力は 3次元の配列
(チャンネル数 × 高さ × 幅) であった。さらに PyTorch では
後で述べる理由により、ひとつのミニバッチの入力を
まるごとひとつの Tensor で表すことが多い。
このような場合、テンソルは4次元の配列
(データ数N × チャンネル数C × 高さH × 幅W) を表すことになる。
このような高次元の配列を頭の中で想像するひとつの方法として、 計算機科学でよく出てくる「木構造」として考えるやりかたがある。 たとえば N×C×H×Wの 4次元テンソルは、 以下のような木構造のいずれかとして解釈できる:
| N × 3次元配列 | N × C × 2次元配列 | N × C × H × W |
Tensorの演算も ndarray型と同じく、
分配 (broadcast) と
要素ごとの演算 (element-wise) が
サポートされている。
>>> 5 + torch.tensor([1,2,3]) # 左→右に分配 (broadcast)。 tensor([6, 7, 8]) >>> torch.tensor([1,2,3]) * 5 # 左←右に分配 (broadcast)。 tensor([ 5, 10, 15]) >>> 5 + torch.tensor([[1,2,3], [4,5,6]]) # 行と列に分配。 tensor([[ 6, 7, 8], [ 9, 10, 11]]) >>> torch.tensor([1,2,3]) + torch.tensor([4,5,6]) # 要素ごと (element-wise)。 tensor([5, 7, 9]) >>> torch.tensor([[-1],[1]]) * torch.tensor([[1,2,3], [4,5,6]]) tensor([[-1, -2, -3], [ 4, 5, 6]])
Tensorの参照・変更も、
ndarray とまったく同じである:
x[i][j] とともに x[i,j] という表記も許されている。
>>> x = torch.tensor([[1,2,3], [4,5,6]]) >>> x[0] # 0行目を取得。 tensor([1, 2, 3]) >>> x[1][2] # 1行2列目の値を取得。 6 >>> x[1][1:3] # 1行1〜2列目の値を取得。 tensor([5, 6]) >>> x[1,2] # 上と同じ。 6 >>> x[0,1] = 0 # 0行1列目の値を変更。 >>> x tensor([[1, 0, 3], [4, 5, 6]])
配列の大きさ確認や形状変換なども同じである:
>>> x = torch.tensor([[1,2,3], [4,5,6]]) >>> len(x) # リストとして見たときの要素数 (行数)。 2 >>> x.shape # 配列の「形状」。 (2, 3) >>> x.reshape(3,2) # 3行×2列の配列に変換。 tensor([[1, 2], [3, 4], [5, 6]]) >>> x.reshape(6) # フラットな1次元配列に変換。 tensor([1, 2, 3, 4, 5, 6])
また、Tensorと ndarray配列は
相互に変換することが可能である:
>>> np.array(torch.tensor([1,2,3])) # Tensorをndarrayに変換。 array([1, 2, 3]) >>> torch.tensor(np.array([1,2,3])) # ndarrayをTensorに変換。 tensor([1, 2, 3])
以下の Tensorの演算をしたときの結果を予想し、
実際に実行してみて結果を確認せよ。
>>> torch.tensor([1,2]) * torch.tensor([3,4]) >>> torch.tensor([1,2]) * 4 >>> torch.tensor([[1,2], [3,4]]) + torch.tensor([[5,6], [7,8]]) >>> torch.tensor([[1],[2],[3]]) * torch.tensor([1,2,3]) >>> torch.tensor([1,2]) * torch.tensor([3]) >>> torch.tensor([1,2]) * torch.tensor([3, 4, 5])
高次元のテンソルを扱うと、しばしば「次元」の順序が重要となってくる。 たとえば、PyTorch では画像をテンソルとして扱う場合 (チャンネル数C × 高さH × 幅W) と表現するのが普通だが、 通常の RGB画像フォーマットではこれは (高さH × 幅W × チャンネル数C) と表現されることが多い:
| 通常のRGB画像 | PyTorchにおける表現 |
|---|---|
[ [[R G B] [R G B] ... [R G B]] [[R G B] [R G B] ... [R G B]] ... [[R G B] [R G B] ... [R G B]] ] |
[ [[R R ... R] [[G G ... G] [[B B ... B]
[R R ... R] [G G ... G] [B B ... B]
... ... ...
[R R ... R]] [G G ... G]] [B B ... B]] ]
|
PyTorch で普通に (Pillow などのライブラリを使って) 画像ファイルを処理しようとすると、要素の並び方がネットワークの想定と違う場合が出てくる。 そのため PyTorch の Tensor では、次元の「並び換え (permute)」という操作が可能である。 (類似の処理に「転置 (transpose)」があるが、permute のほうが汎用性があるため、 こちらを紹介する。)
permute()メソッドの使い方は簡単で、もとの次元の番号
(0, 1, 2, ...) を並び換えたい順序で指定すればよい。
テンソルの各要素を指定された順序で並び換えた新しい Tensor が返される。
# (2×2×3) のテンソルを作成。 >>> x = torch.tensor([ [[1,2,3], [1,2,3]], [[4,5,6],[4,5,6]] ]) # (0,1,2)番目の次元を、それぞれ(1,0,2)番目に並び換える。 >>> x.permute(1,0,2) tensor([[[1, 2, 3], [4, 5, 6]], [[1, 2, 3], [4, 5, 6]]])
N枚の画像データが (N × W × H × C) というテンソルで表されているとする。
これを PyTorch の (N × C × H × W) というテンソルに変換するための
permute() の引数を答えよ。
Tensorには、勾配を自動的に計算する機能がある。
この機能を使うには、まず勾配を計算したい Tensor を作成するときに
requires_grad=True オプションを渡しておく。
このテンソルを使って何がしかの計算をおこなった後、
その結果のテンソルに対して backward() メソッドを呼ぶと、
計算に使ったテンソルすべての勾配が計算される。
これは、各テンソルが使われた計算過程 (計算グラフ) をすべて記録しているためである。
たとえば以下の例では関数 y = x3 + 2x + 1 の x = 1 における
微分 dy/dx (x.grad) を求めている:
>>> x = torch.tensor(1.0, requires_grad=True) >>> y = x**3 + 2*x + 1 # y = x3 + 2x + 1 を計算。 >>> y tensor(4., grad_fn=<AddBackward0>) >>> y.backward() # dy/dx を計算。 >>> x.grad # dy/dx を表示。 tensor(5.) >>> y = x**3 + 2*x + 1 # もう一度計算。 >>> y.backward() >>> x.grad tensor(10.) # 値が増えている。 >>> x.grad = None # 勾配をクリアする。
上の例でわかるように、各 Tensor に付随する勾配 (.gradの値) は
backward() を実行するたびに毎回上書きされるのではなく、
以前の値に足されるようになっている。これはニューラルネットワークの
誤差逆伝播法においては、複数のノードからくる勾配を足し合わせるためである。
勾配をゼロにクリアするときは x.grad = None のようにする。
(注意: .grad はつねに Tensor型でなければならないため、
x.grad = 0 とはできない。)
PyTorch を通常使っている限りでは、勾配を直接利用することはほとんどないが、
つねに勾配が失われないように注意する必要がある。
たとえば以下の例で、平方根を計算するのに Python 組み込みの
math.sqrt() 関数を使うと、Tensorが
通常の float型に変換されてしまい、その計算過程は失われ、
勾配が計算できなくなってしまう。
勾配を保持するには、つねに PyTorch の組み込み関数
(torch.sqrt() など) を使って演算する必要がある。
このため PyTorch はほぼすべての演算に対して自前のバージョンを用意している。
>>> x = torch.tensor(2.0, requires_grad=True) >>> y = math.sqrt(x) # math.sqrt() は Tensor を通常の値に変換してしまう。 >>> y 1.4142135623730951 >>> y = torch.sqrt(x) # torch.sqrt() は Tensor のままで計算する。 >>> y tensor(1.4142, grad_fn=<SqrtBackward>)
NumPy では、ndarray では配列の各要素は
「通常の (int型などの) 数値」であったが、
PyTorch では Tensor の各要素も Tensorである。
これは、すべての値が勾配を保持できるようにするためである。
ひとつの数値をあらわすテンソルは「0次元のTensor」として
表されるが、これを意図的に「ただの数値」に変換するためには、
.item() メソッドを使えばよい。
当然ながら、こうすると勾配は失われてしまうので注意。
>>> a = np.array([1,2,3]) >>> a[1] # ndarrayの要素を取得。 2 >>> x = torch.tensor([1,2,3]) >>> x[1] # Tensorの要素を取得。 tensor(2) >>> x[1].item() # Tensorの要素を通常の数値に変換。(勾配は失われる) 2
PyTorch で CUDA が使用可能な場合、Tensor を
GPU 上に転送し、そこで計算させることができる。
Tensorに対して .to('cuda')メソッドを実行すると
そのテンソルは GPU 上に転送され、逆に .to('cpu')メソッドを実行すると
GPU上のテンソルが CPU に転送される:
>>> torch.cuda.is_available() True # CUDAが利用可能。 >>> x1 = torch.tensor([1,2,3]) # x1はCPU上に作成される。 >>> x1 tensor([1, 2, 3]) >>> x2 = x1.to('cuda') # x1をGPUに転送し、x2とする。 >>> x2 tensor([1, 2, 3], device='cuda:0') >>> x3 = x2.to('cpu') # x2をCPUに転送し、x3とする。 >>> x3 tensor([1, 4, 9])
GPU 上にある Tensorどうしを計算しようとすると、 自動的に GPU 内で計算が行われ、結果も GPU 上のテンソルとして返される。 いっぽう、CPU と GPU 内にある Tensorは互いに計算できない:
>>> x2*x2 # GPU上で計算をおこなう。 tensor([1, 4, 9], device='cuda:0') >>> x1*x2 # CPU上とGPU上にあるデータは互いに計算できない。 RuntimeError: Expected all tensors to be on the same device, but found at least two devices, cuda:0 and cpu!
基本的には、PyTorch で GPU を使う際にはほとんど何もする必要がない。
何か複雑な計算を行う直前に Tensor を .to('cuda') で GPUに転送しておき、
計算が終わったらその結果を .to('cpu') で受け取ればよいのである。
GPU内での演算は内部で CUDA用のコードが自動的に生成・実行されるが、
ユーザはそのことを気にする必要がない。
以下のプログラムを実行し、表示された時間を観察せよ。
つぎに .to('cuda') の部分を
はずして CPU 上で実行し、GPU と比べて何倍の時間がかかったかを調べよ。
import time # timeit: テンソルを二乗し、計算にかかった時間を表示する。 def timeit(x): t0 = time.time() x = torch.mm(x, x) dt = time.time() - t0 print(dt) return dt # 100×100のランダムな行列を二乗する。 x = torch.rand(100,100).to('cuda') timeit(x) # 10000×10000のランダムな行列を二乗する。 x = torch.rand(10000,10000).to('cuda') timeit(x)
以上をふまえて、PyTorch におけるニューラルネットワーク学習の おおまかな流れを説明する。はじめに、これまで実装してきた ニューラルネットワークと PyTorch の実装は若干異なっている:
PyTorch による学習の流れを図示すると、以下のようになる:
実際のコードは以下のようになっている:
# ニューラルネットワークを定義する。 model = ... # ニューラルネットワークを訓練モードにする。 model.train() # ミニバッチごとの訓練データを用意する。 minibatches = [ ... ] # 最適化器と学習率を定義する。 optimizer = optim.SGD(model.parameters(), lr=0.01) # 各ミニバッチを処理する。 for (inputs, targets) in minibatches: # すべての勾配(.grad)をクリアしておく。 optimizer.zero_grad() # 与えられたミニバッチをニューラルネットワークに処理させる。 output = model(inputs) # 損失を計算する。 loss = F.mse_loss(output, targets) # 勾配を計算する。 loss.backward() # 重み・バイアスを更新する。 optimizer.step()
PyTorch のコードは大抵どれもこのパターンに従っている。
違うのは最適化器と学習率および損失関数で、
上の例ではそれぞれ最適化器として optim.SGD (普通の確率的勾配降下法)、
学習率 0.01、
そして損失関数として F.mse_loss を使っている。
(PyTorchでは、ニューラルネットワーク用の関数は
すべて F. という名前空間で定義される慣例になっている。)
では前章で NumPy を使って実装した MNIST を、 今回は PyTorch を使って実装してみよう。
まず、ニューラルネットワークを定義する部分である:
import torch import torch.nn as nn import torch.nn.functional as F import torch.optim as optim # MNISTを処理するニューラルネットワーク。 class MNISTNet(nn.Module): # 各レイヤーの初期化。 def __init__(self): nn.Module.__init__(self) # 畳み込み: 入力1チャンネル、出力10チャンネル、カーネル3×3。 self.conv1 = nn.Conv2d(1, 10, 3) # Max Pooling: 1/2に縮める。 self.pool1 = nn.MaxPool2d(2) # 畳み込み: 入力10チャンネル、出力20チャンネル、カーネル3×3。 self.conv2 = nn.Conv2d(10, 20, 3) # Max Pooling: 1/2に縮める。 self.pool2 = nn.MaxPool2d(2) # 全接続 (fully connected): 入力500ノード、出力10ノード。 self.fc1 = nn.Linear(20*5*5, 10) return # 与えらえたミニバッチ x を処理する。 def forward(self, x): # x: (N × 1 × 28 × 28) x = self.conv1(x) x = F.relu(x) # x: (N × 10 × 26 × 26) x = self.pool1(x) # x: (N × 10 × 13 × 13) x = self.conv2(x) x = F.relu(x) # x: (N × 20 × 11 × 11) x = self.pool2(x) # x: (N × 20 × 5 × 5) x = x.reshape(len(x), 20*5*5) # x: (N × 500) x = self.fc1(x) # x: (N × 10) return x # 実際のインスタンスを作成。 model = MNISTNet()
まず、PyTorch におけるニューラルネットワークは、すべて
nn.Module の派生クラスとして定義する。
この中で各レイヤーの初期化をおこなう __init__() メソッドと、
入力から出力までの処理をおこなう forward() メソッドを実装している。
以下、順に見ていこう。
__init__() メソッドでは、 nn.Conv2d,
nn.MaxPool2d などのインスタンスを作成している。
PyTorch では、これらは最初からニューラルネットワークの構成レイヤーとして
利用可能である:
nn.Linear(入力ノード数, 出力ノード数)
… 全接続レイヤーを作成する。
nn.Conv2d(入力チャンネル数, 出力チャンネル数, カーネル幅)
… 畳み込みレイヤーを作成する。
nn.MaxPool2d(カーネル幅)
… Max poolingレイヤーを作成する。カーネル幅は縮小率を表す。
nn.Linear および nn.Conv2d インスタンスはどちらも
内部に重み・バイアスを保持しており、これらはインスタンス作成時に
ランダムに初期化されている。
次の forward() メソッドは、
前に NumPy などで実装した forward() メソッドとほぼ同じである。
入力値として Tensorの x が与えられ、
それを各レイヤーに通して最終的な出力テンソルを返す。
PyTorch では、各レイヤーは「関数呼び出しのように」利用する流儀になっている:
上の例で使われているx = self.conv1(x) # 正しい x = self.conv1.forward(x) # 間違い
F.relu() は ReLU 関数である。
最後のレイヤー fc1 のあとでは活性化関数を適用していないが、
PyTorch では慣例により、最終レイヤーの活性化関数は
forward() の外側で適用することになっている。
PyTorch では、nn.Module の派生クラス
(nn.Linear や nn.Conv2d も含む) はすべて
forward() メソッドを持っているが、これらを直接呼び出すことはなく、
つねに関数呼び出しのように利用する
(これは Python における __call__ メソッドを使っている)。
MNISTNet インスタンス自身も nn.Module の派生クラスなので、
forward() メソッドを直接呼び出すことはなく、関数呼び出しのように利用する:
# ニューラルネットワークを定義する。 model = MNISTNet() # ニューラルネットワークを使用する。(x: 入力テンソル) x = model(x)
つまり PyTorch におけるニューラルネットワークは、
入れ子になった nn.Moduleクラス (の派生クラス) と考えることができる:
なお、ここで作成した MNISTNet インスタンスを表示すると、
内部の構造を実際に見ることができる:
>>> print(model) MNISTNet( (conv1): Conv2d(1, 10, kernel_size=(3, 3), stride=(1, 1)) (pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) (conv2): Conv2d(10, 20, kernel_size=(3, 3), stride=(1, 1)) (pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) (fc1): Linear(in_features=500, out_features=10, bias=True) )
では、実際にこのモデルを使って学習をおこなってみる。 以下のコードは、2.5 節で示したものとほとんど同じである:
# ミニバッチごとの訓練データを用意する。 train_images = splitarray3d(32, load_mnist('train-images-idx3-ubyte.gz')) train_labels = splitarray1d(32, load_mnist('train-labels-idx1-ubyte.gz')) # ニューラルネットワークを訓練モードにする。 model.train() # 最適化器と学習率を定義する。 optimizer = optim.SGD(model.parameters(), lr=0.01) n = 0 # 各ミニバッチを処理する。 for (images,labels) in zip(train_images, train_labels): images = images.reshape(len(images), 1, 28, 28) # 入力をfloat型のテンソルに変換。 inputs = torch.tensor(images).float() # 正解をlong型のテンソルに変換。 targets = torch.tensor(labels).long() # すべての勾配(.grad)をクリアしておく。 optimizer.zero_grad() # 与えられたミニバッチをニューラルネットワークに処理させる。 output = model(inputs) # 損失を計算する。 loss = F.cross_entropy(output, labels) # 勾配を計算する。 loss.backward() # 重み・バイアスを更新する。 optimizer.step() n += len(images) print(n, loss.item())
上のコードで使っている F.cross_entropy() という関数は
交差エントロピー誤差を計算するもので、実際には
と等価である (loss = F.nll_loss(F.log_softmax(output, dim=1), labels)
F.log_softmax() の最後に dim=1 という
部分があるが、これは入力が (N×10) の2次元配列なので、
2番目の次元に対して LogSoftmax 関数を適用せよという意味である。)
また、訓練データをミニバッチごとに区切るため
splitarray3d() と splitarray1d() という関数を使っている:
# splitarray1d: 与えられて1次元配列をn要素ごとに区切る。 def splitarray1d(n, a): for i in range(0, len(a), n): yield np.array(a[i:i+n]) return # splitarray3d: 与えられて3次元配列をn要素ごとに区切る。 def splitarray3d(n, a): for i in range(0, len(a), n): yield np.array(a[i:i+n,:,:]) return
訓練したニューラルネットワークを評価するには、 以下のようにする。ここでもミニバッチごとに評価している以外は、 以前のコードとほどんど変わっていない。
# ミニバッチごとのテストデータを用意する。 test_images = splitarray3d(32, load_mnist('t10k-images-idx3-ubyte.gz')) test_labels = splitarray1d(32, load_mnist('t10k-labels-idx1-ubyte.gz')) # ニューラルネットワークを評価モードにする。 model.eval() correct = 0 for (images,labels) in zip(test_images, test_labels): images = images.reshape(len(images), 1, 28, 28) # 入力をfloat型のテンソルに変換。 inputs = torch.tensor(images).float() # 与えられたミニバッチをニューラルネットワークに処理させる。 outputs = model(inputs) # 正解かどうかを判定する。 for (y,label) in zip(outputs, labels): i = torch.argmax(y) if i == label: correct += 1 print(correct)
上のコード中に「ニューラルネットワークを訓練モードに」
model.train()
「評価モードに」
model.eval()
という部分があるが、これは PyTorch における
一部のレイヤー (後で説明する BatchNorm など) の挙動が
訓練時と推論時で変わるためである。
とりあえず、これは PyTorch を使ううえでの
慣例であると覚えておけばよい。
上のコード mnist_dl.py を実際に動かし、
実行時間を計測せよ。
PyTorch を使うと、(たとえ GPU を使わずとも) NumPy よりもずっと高速に処理できることがわかる。 これはフレームワーク全体がニューラルネットワークの処理のみに 特化されているためである。
PyTorch には、他にもニューラルネットワークの実験用に 便利な機能がいろいろ用意されている。そのうちのひとつが 学習したモデル (重み・バイアス) のファイルへの保存機能である。 NumPy を使った例では、訓練したニューラルネットワークの 重み・バイアスはメモリ上にある状態のままで使っていたが、 実際にはこれをファイルに保存しておき、あとで読み込みたい。 PyTorch ではこれを以下のように簡単に行うことができる:
model = MNISTNet() # ニューラルネットワークを訓練する。 model.train() ... # 訓練した重み・バイアスをファイルに保存する。 torch.save(model.state_dict(), 'model.pt')
model = MNISTNet() # 保存しておいた重み・バイアスを読み込む。 model.load_state_dict(torch.load('model.pt')) # ニューラルネットワークを使用する。 model.eval() ...
ここで model.state_dict() メソッドは、
MNISTNet クラス内部で定義されている
各レイヤー (nn.Conv2d、nn.Linear) の
重み・バイアスを再帰的に列挙し、
ひとつの巨大な Python 辞書として返すものである。
nn.Moduleクラス (ここでは MNISTNet クラス) および
model.load_state_dict() メソッドはその逆で、
Python 辞書として与えられた重み・バイアスを Moduleクラス中の
各レイヤーに設定する。
これらのメソッドは Pythonのリフレクション機能を利用しているため、
トップレベルの Moduleクラスのみに適用すれば
再帰的に内部の Moduleクラスも処理されるようになっている。
なお、2.5 節で使われていた
model.parameters() も
類似の仕組みで作られており、これは Moduleクラス内で
使われている重み・バイアスを列挙し、一括して
optimizerインスタンスに渡せるようになっている。
さて、これまで説明してきた方法はすべて CPU を使ったものであった。 PyTorch では、計算に使うテンソルが GPU 上にあれば GPU 上で計算が行われる。 そのため、以上のコードを GPU に対応させるのは容易である。 具体的には、以下のステップを踏めさえすればよい:
# model = MNISTNet()
model = MNISTNet().to('cuda')
inputs = inputs.to('cuda')
outputs = model(inputs)
outputs = outputs.to('cpu')
mnist_dl.py が GPU 上で動くように変更せよ。
ここで、PyTorch でよく使われる
Dataset クラスと DataLoader クラスについて、
簡単に説明しておく。ミニバッチを使った学習では、訓練データが
ミニバッチ中になるべくランダムな順序で現れるようにする必要があるが、
これら 2つのクラスを使うと、訓練データを簡単にミニバッチに区切ったり、
シャッフルしたりすることができる。
まず、Datasetクラスを継承して MNISTDataset を定義する。
ここでは __len__() と __getitem__() という
2つのメソッドのみを定義しておく。Python ではこれらのメソッドを上書きすることで、
そのインスタンスを配列のように扱うことができる:
from torch.utils.data import Dataset, DataLoader ## MNISTDataset ## 指定されたファイルから入力と正解を読み込む。 ## class MNISTDataset(Dataset): def __init__(self, images_path, labels_path): # データセットを初期化する。 Dataset.__init__(self) self.images = load_mnist(images_path) self.labels = load_mnist(labels_path) return def __len__(self): # データの個数を返す。 return len(self.images) def __getitem__(self, i): # i番目の (入力, 正解) タプルを返す。 return (self.images[i], self.labels[i]) # 実際のインスタンスを作成。 dataset = MNISTDataset('t10k-images-idx3-ubyte.gz', 't10k-labels-idx1-ubyte.gz') print(len(dataset)) # データの個数を返す。 print(dataset[0]) # 0番目の (入力, 正解) タプルを返す。
上のようなクラスを定義しておくと、これに対して
DataLoaderクラスを使うことができる。
DataLoader クラスは Dataset が提供する
各データをシャッフルし、ミニバッチごとに返す。
あとはこれを使って訓練すればよい:
# バッチサイズ32 でデータを利用する。 loader = DataLoader(dataset, batch_size=32) for (images, labels) in loader: # images: 32個の入力画像 # labels: 32個の正解ラベル ...
PyTorch でもうひとつの便利な機能として、Adam最適化器が 利用可能なことがあげられる。Adam は従来の単純な勾配降下法 (SGD) を 改良した方法で、SGD に比べてより早く収束する (重み・バイアスが学習できる) ことが知られている。
Adam の簡単な原理は次のとおりである。従来の SGD では、 勾配の各成分に決まった学習率 (alpha) を掛けて重み・バイアスを調整していた:
# 単純なSGD
w1 -= alpha * dw1
w2 -= alpha * dw2
w3 -= alpha * dw3
...
Adam では、これに以下のような改良が加えられている (詳細は省略):
PyTorch で SGD の代わりに Adam を使うには、 次の1行を書き換えるだけでよい:
# 最適化器と学習率を定義する。 # optimizer = optim.SGD(model.parameters(), lr=0.01) optimizer = optim.Adam(model.parameters(), lr=0.01)
以上で説明してきた PyTorch によるニューラルネットワークの構築、 モデルの保存・読み込み、GPU の利用などをすべてまとめ、 MNIST を PyTorch で実験をおこなうさいの典型的な形式にしたものが mnist_torch.py である。 これは、今後いろいろなモデルを使って機械学習の実験をおこなうための 雛形として利用することができる。
mnist_torch.py の構成は以下のようになっている:
# 必要なモジュールのインポート import torch ... # Datasetの定義 class MNISTDataset(Dataset): ... # モデルの定義 class MNISTNet(nn.Module): ... # train: 1エポック分の訓練をおこなう関数。 def train(model, device, loader, optimizer, ...): ... # test: テストをおこなう関数。 def test(model, device, loader): ... # main: 最初に実行される関数。 def main(): ... if __name__ == '__main__': main()
main() 関数は、argparseモジュールを
使ってコマンドライン引数を解析する。コマンドラインの書き方は
多くの PyTorch用のプログラムで共通しており、
以下のような書式になっている
(この説明は -h オプションを与えると表示される):
usage: mnist_torch.py
[-h] [--verbose] [--batch-size N] [--test-batch-size N]
[--no-shuffle] [--epochs N] [--lr LR] [--seed S]
[--no-cuda] [--dry-run] [--log-interval N]
[--save-model path]
datadir
最後の引数 datadir は必須で、
ここには MNIST のデータ (train-images-idx3-ubyte.gz および
train-labels-idx1-ubyte.gz) が入っている
ディレクトリのパスを指定する。それ以外のオプションの説明は
以下のとおりである:
| オプション | 説明 |
|---|---|
--verbose |
詳細なログを表示する。 |
--batch-size n |
訓練時のバッチサイズを指定する。(デフォルト: 32個) |
--test-batch-size n |
テスト時のバッチサイズを指定する。(デフォルト: 1000個) |
--no-shuffle |
訓練データをシャッフルしない。 |
--epochs N |
訓練時のエポック数を指定する。(デフォルト: 10回) |
--lr rate |
学習率を指定する。(デフォルト: 0.01) |
--seed seed |
乱数のシードを指定する。(デフォルト: 1) |
--no-cuda |
GPUがある場合でもCUDAを使用しない。 |
--dry-run |
デバッグ用に1バッチのみ実行する。 |
--log-interval n |
進捗状況を表示する間隔。(デフォルト: 10バッチごと) |
--save-model path |
モデルを保存・読み込むパス名。(デフォルト: なし) |
--verbose や --no-cuda、
--dry-run などのオプションは、プログラムの
デバッグ時に用いる。それ以外のオプションは条件をあれこれ変えて
実験したいときに利用する。たとえば、訓練データ・テストデータが
./MNIST ディレクトリに入っているとして、学習率 0.005 で
100エポックの訓練をおこない、完了時のモデルを mnist_net.pt
というファイルに保存したい場合は、以下のようにする:
$ python mnist_torch.py --lr=0.005 --epochs=100 --save-model=mnist_net.pt ./MNIST
mnist_torch.py のコードを参考に、
CIFAR-10 を PyTorch 上で実装せよ。
nn.Linear レイヤーや
nn.Conv2d レイヤー、活性化関数などを
組み合わせてニューラルネットワークを構築する。