2. CFL-Reachability って何?
- あるノードからあるノードまでの経路 (path) をさがす。
ただし各エッジは指定された順序でしかたどれない。
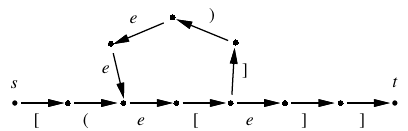
- 順序は文脈自由言語 (CFL) で表現される。
= 文脈自由文法 (CFG) で生成される文字列の集合。 - ある言語 L を満たすような経路を L-path とよぶ。
|
Program Analysis via Graph Reachability
Thomas Reps |
[(e[])eee[e]] を解析し、構文木を書け。
L: matched → matched matched
| ( matched )
| [ matched ]
| e
| ε (空列)
while (true) {
for e2,e2 in 隣りあったエッジ {
if (規則 A → e2 e3 がある) {
新しいエッジ A を追加。
}
}
if (これ以上追加できない) { break; }
}
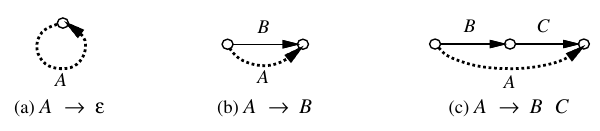
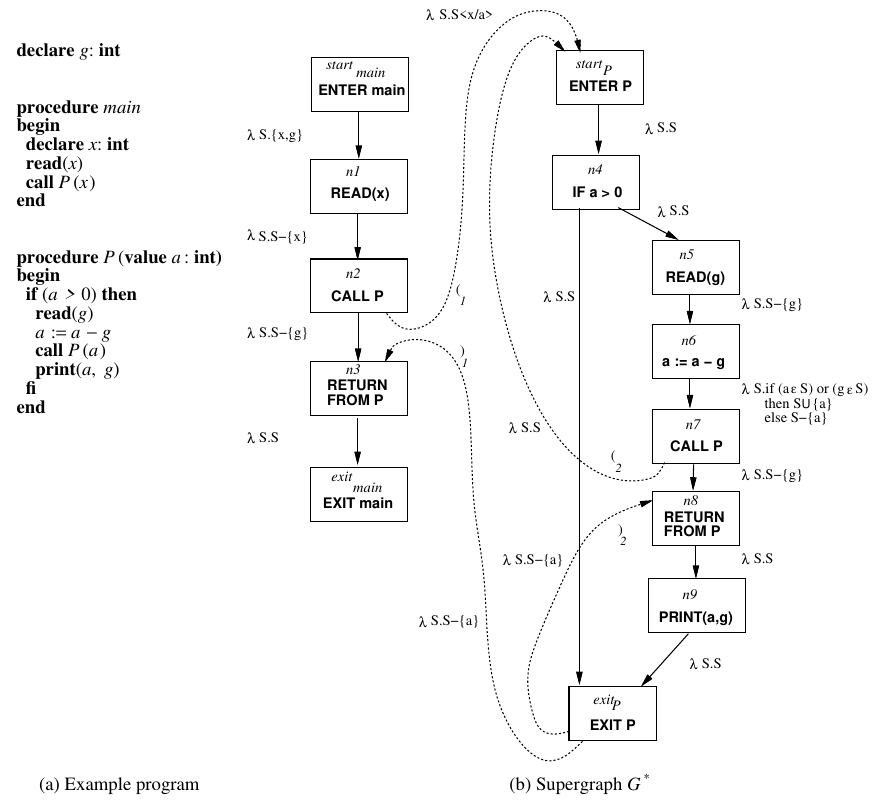
matched → matched matched
| (i matched )i
| e
| ε
realizable → matched realizable
| (i realizable
| ε
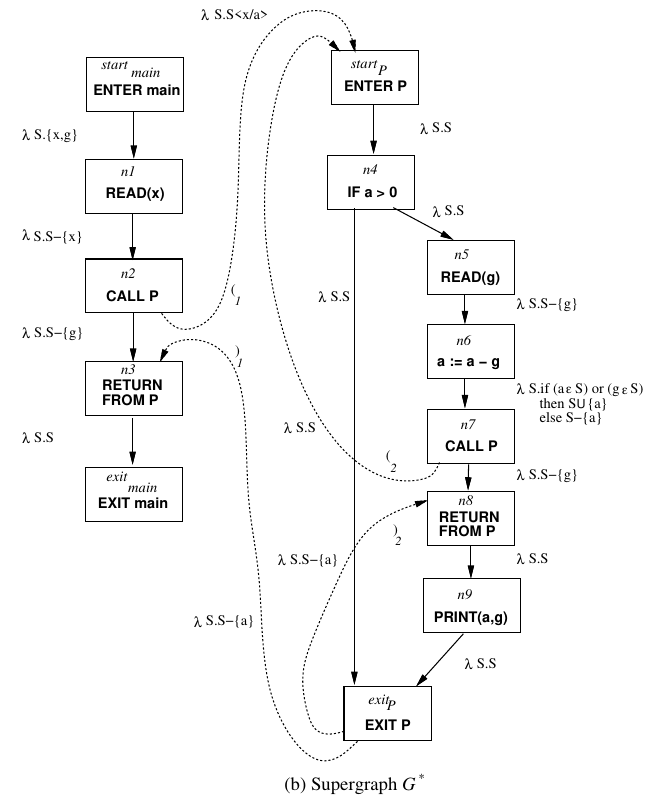
e e (1 e
e e (1 e e )1
e e (1 e e )2
e e (1 e
e e (1 e e )1
e e (1 e e )2
main から実際に呼ばれうる経路のみを考慮)
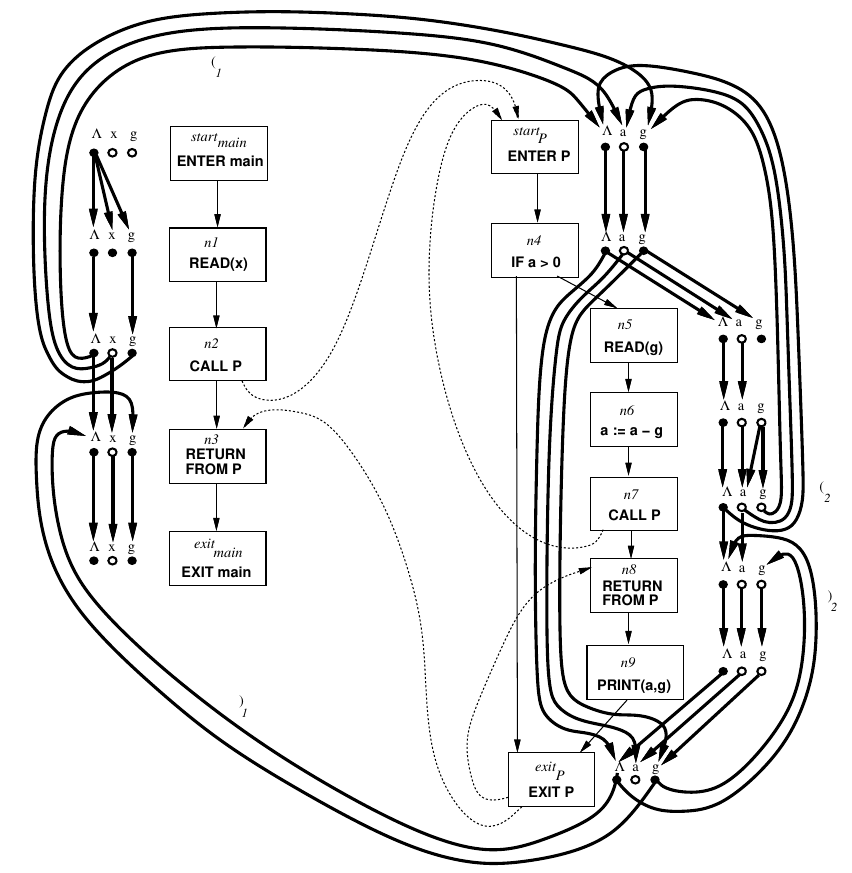
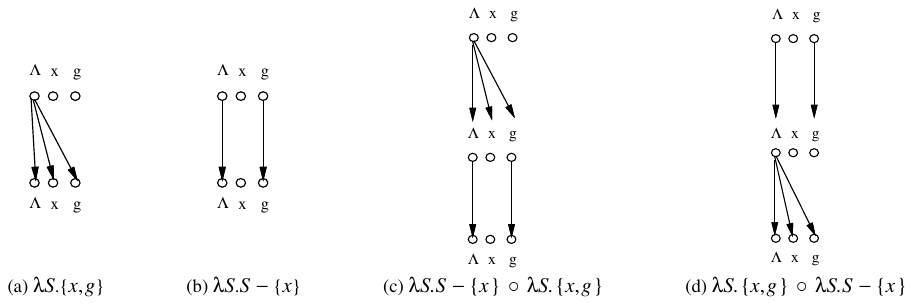
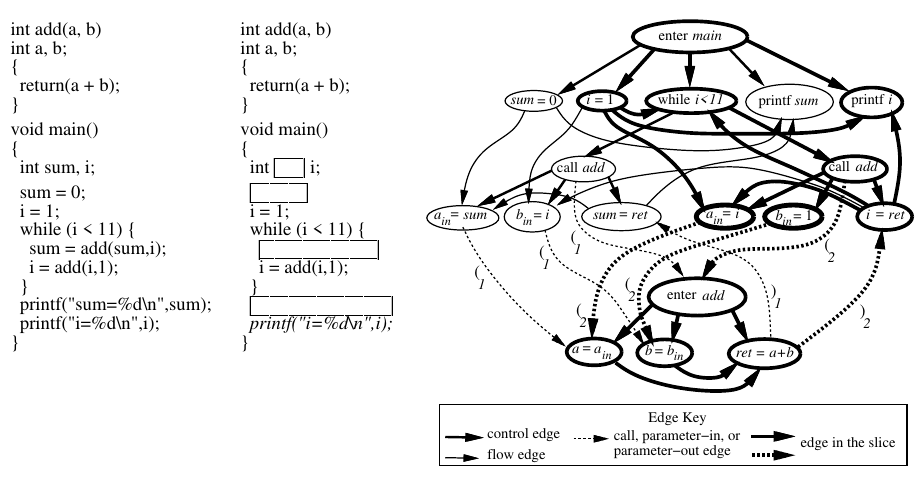
unbalanced-right → unbalanced-right matched
| unbalanced-right )i
| ε
slice → unbalanced-right realizable
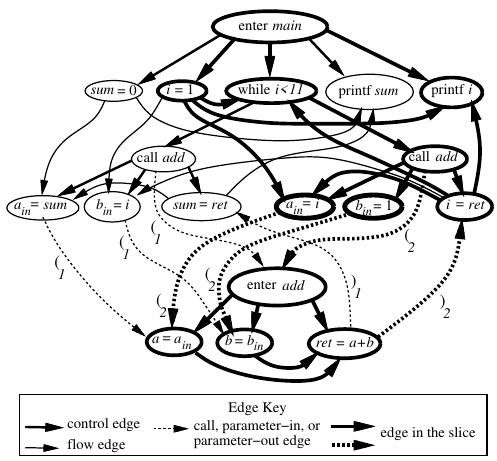
printf i に到達する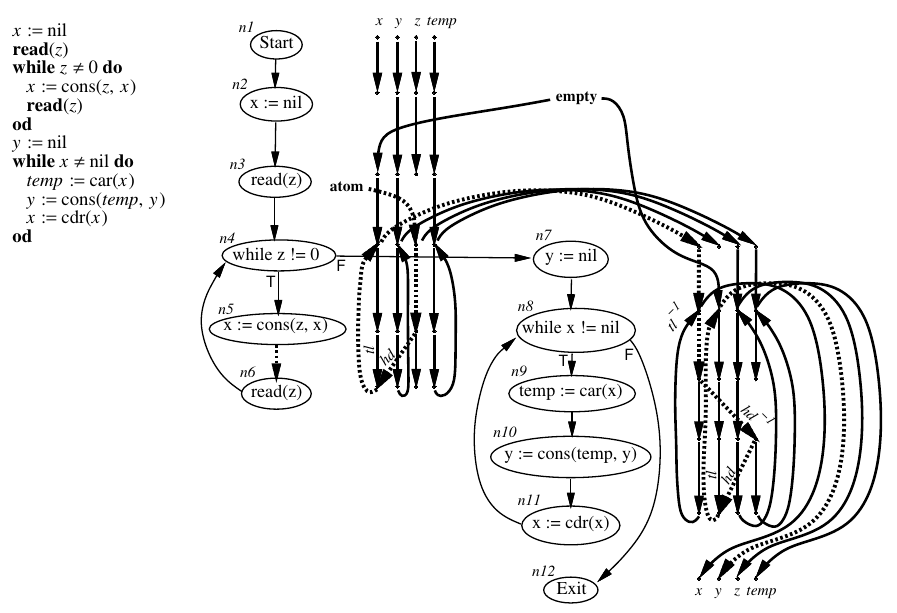
| (nop) | x=nil; | z=cons(x,y); | x=y; | x=car(y); | x=cdr(y); |
id_path → id_path id_path
| hd id_path hd-1
| tl id_path tl-1
| id
| ε
hd_path → id_path hd id_path tl_path → id_path tl id_path
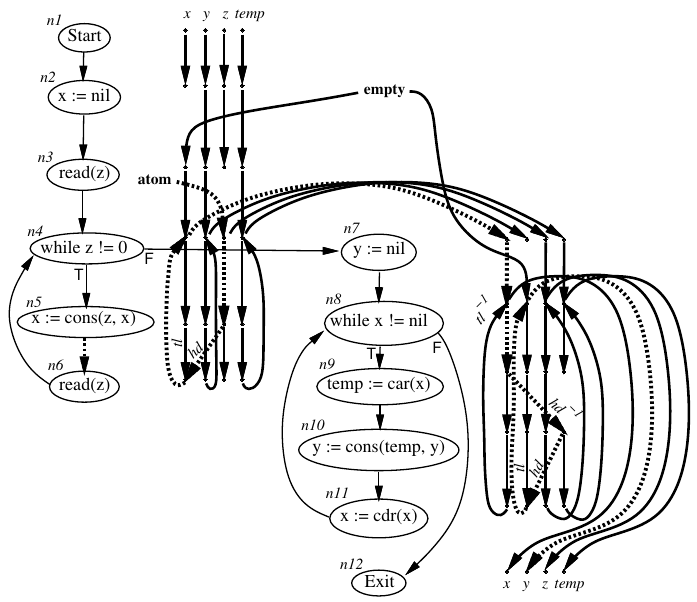
empty
atom,empty)
p=&q; p=q; p=*q; *p=q;
malloc() はつねに同じアドレスを返すとする。
p = malloc();
→ p = &malloc_s;
p = &q; |
assignAddr(p, q). |
p = q; |
assign(p, q). |
p = *q; |
assignStar(p, q). |
*p = q; |
starAssign(p, q). |
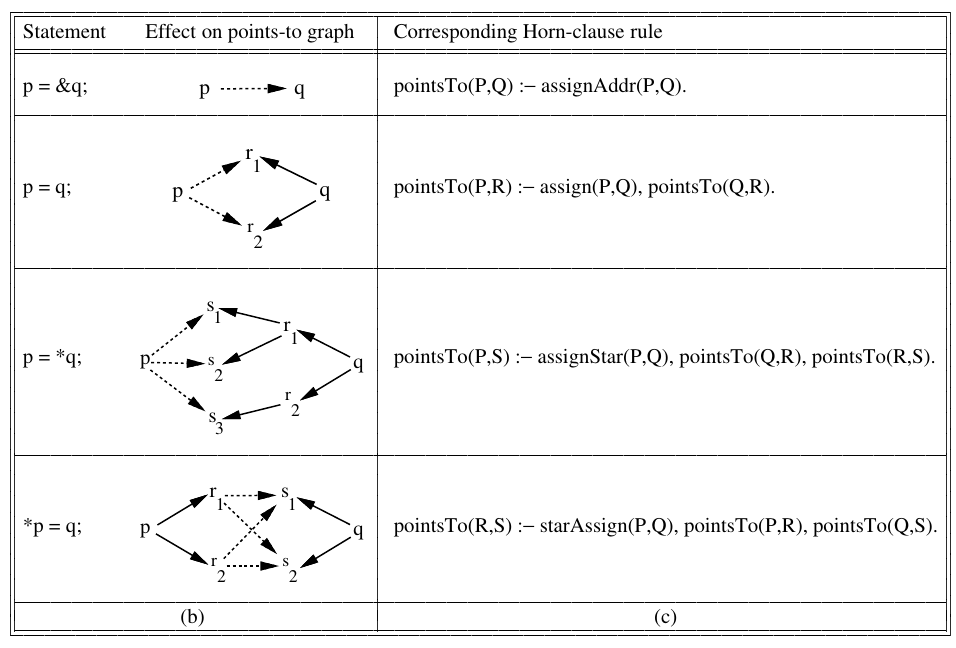
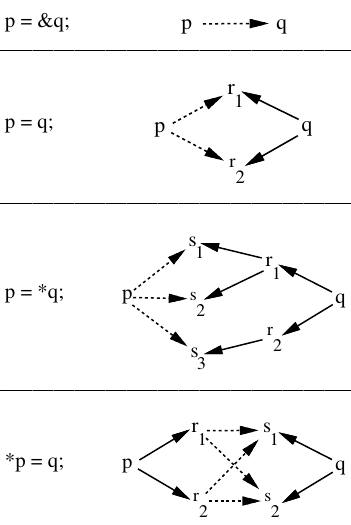
a = &b; d = &c; d = a; e = &a; *e = d; f = *e;
| → |
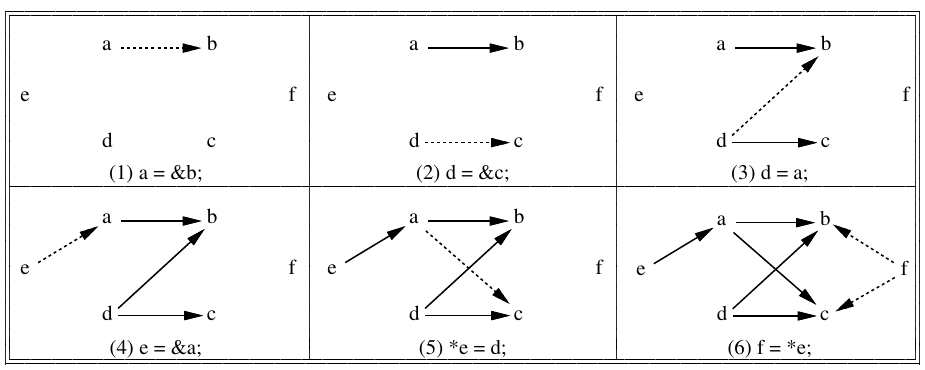
p = &q; |
assignAddr(p, q). | assignAddr(q, p). |
p = q; |
assign(p, q). | assign(q, p). |
p = *q; |
assignStar(p, q). | assignStar(q, p). |
*p = q; |
starAssign(p, q). | starAssign(q, p). |
| pointsTo → assignAddr |
| pointsTo → assignAddr |
| pointsTo → assign pointsTo |
| pointsTo → pointsTo assign |
| pointsTo → assignStar pointsTo pointsTo |
| pointsTo → pointsTo pointsTo assignStar |
| pointsTo → pointsTo starAssign pointsTo |
| pointsTo → pointsTo starAssign pointsTo |
f が b および c を
指しうることを示せ。
|
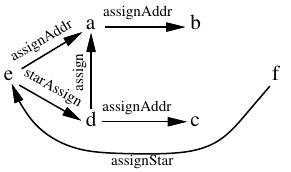
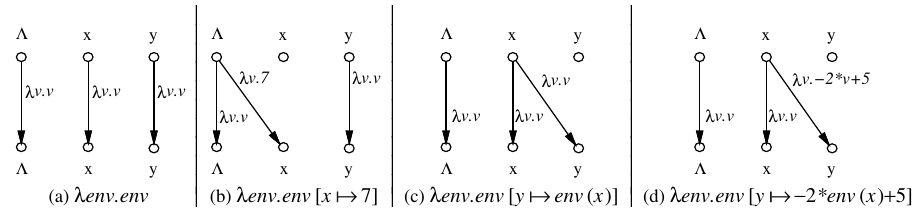
新山の 研究テーマについて |
f(X) {
y ← +∞
for each x in X {
if x < y {
y ← x
}
}
return y
}
class Range {
int vMin;
int vMax;
}
f(int v) {
a = v - vMax;
b = vMin - v;
return max(max(a, b), 0);
}
int pow(int x, int y) {
int z = 1;
while (0 < y) {
z *= x;
y -= 1;
}
return z;
}
