ここでは、p個のパラメータ X1, X2, ... Xp から観測された変数 Y を、 p よりも少ない M個の変数 Z1, Z2, ... ZM の線形和で表現することを考える:
このとき、Y はこうなる:
ここで θ0, θ1, ..., θM は 線型回帰の係数である。もし、 φ1m, φ2m, ..., φpm の値が うまく選ばれていれば、これを使った最小二乗法の誤差は もとの式の最小二乗法の誤差よりも小さくなるはずである。 ここでは p+1 個の係数を推定するかわりに M+1 個の係数を推定することで「次元の削減」をおこなっている。
ちなみに
主成分分析 (Principal Component Analysis, PCA) は
多変量のデータを少数の素性に分解するポピュラーな手法である。
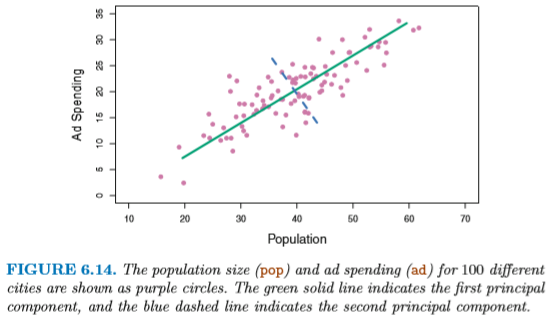
たとえば図 6.14 は各都市の人口 (pop) と広告費 (ad) の
関係にみられる第1主成分 (first principal component) を表している:
これを実際の直線上に分布させてみると、次のようになる。 図6.15の右側は、各点を第1主成分の上に投影 (projection) した 点が示されている。
数学的には、この第1主成分 Z1 は次のように表現される:
pop - Avg(pop )) +
0.544 × (ad - Avg(ad ))
データ上のある点における Z1 の値を、 その点の第1主成分のスコア (first principal component score) とよぶ。 PCA では、スコアの分散が最大になるように変数の組み合わせを求める。 (実際には、係数を大きくすれば分散はいくらでも大きくなってしまうので、 Σ(各係数2) = 1 となるように制限する。)
注意: ここで得られる直線は普通の最小二乗法に近いが、 同じではないことに注意。 最小二乗法は各点と直線との
図 6.16 に示すように、
第1主成分と各変数 pop および ad の
相関はどちらも高い。
pop - Avg(pop )) -
0.839 × (ad - Avg(ad ))
例: p = 2 の場合、Z1 を求めてみると…
これを力ずくで (!) 求めるような実装が以下である (7/17 バグ修正済):
主成分回帰 (Pricipal Component Regression, PCR) とは、まず
主成分分析をおこない、その上位M個の主成分 Z1, ..., ZM に
対して線型回帰を行う方法である。これは、ほとんどのデータの変化は
少数の主成分の変化のみによって説明できるという仮定にもとづいている。
この仮定は必ずしも正しくないが、うまくいくことが多い。
上の広告費データの例では、変数 pop と ad の変化は
ほとんど第1主成分 Z1 の変化によって説明できるので、
ここからさらに別の変数 (sales など) を予測することはたやすい。
ただし、PCR では素性の線形和を求めているだけで、
素性そのものの数を減らしているわけではないことに注意。
この点で、PCR は 6.2.1. 節で説明した "Ridge regression" に近い。(?)
PCR で使用する主成分の個数 M は、
ふつうクロス・バリデーション (cross validation) によって
決定される。たとえば図 6.20 は Creditデータの回帰を
PCR によって (M の数を変化させつつ) 行った結果である。
M = 10 でエラーが最も小さくなっているが、もともとの変数は 11個なので、
これではほとんど次元を削減していることにならない。
PCR の基本アプローチは、入力変数 X の値だけを見て、 主成分を決定するというものであった。 しかし実際には PCA の結果が出力変数 Y と相関しているという保証はない。 そこで、変数 Y の値を見ながら「教示つきで (supervised)」 主成分 Z1, ..., ZM の線形和を決定するのが PLS である。 PLS では、X および Y 両方の変化を 説明するような組み合せを探す。
PLS は以下のようなステップで計算する:
伝統的に、統計で扱うデータは predictor の個数 p が サンプル数 n に比べてはるかに低い (p ≪ n) ものが多かった。 ところが過去20年のうちに、p > n であるようなデータが 扱われるようになった。たとえば:
サンプルの数よりもパラメータ数が多いデータを 「高次元な (high-dimensional)」データという。 過学習 (overfitting) の問題はつねに存在したが、 高次元ではこれがなおさら重要になる。
最小二乗法など多くの統計的手法において、 推定するパラメータ数がサンプル数よりも 多い場合、ほぼつねに「完璧フィット」する解が見つかってしまう (図6.22)。これはほぼ確実に過学習である。 同様のことはロジスティック回帰やLDAなどでも発生する。
図6.23 はこの問題をさらに如実に表している。 n=20 のデータに対して、p の値を 1〜20 まで変化させなて 最小二乗法を行った場合、R2 の値は p が増えるにつれ増加し、MSE は減少する。 すると p が増えたほうがよさそうに見えるが、 実際に独立したテストセットを使った MSE は非常に大きくなる。
この章 (6章) でとりあげた手法はどれも、 モデルの柔軟性を意図的に下げるものであった。 一般的に、使用するデータが高次元になるほどテストデータを使った精度は減少する。 この現象を「次元の呪い (Curse of dimensionality)」とよぶ。 ふつう与えるパラメータは多いほうがモデルが正確になると思いがちだが、 多くは相関のないパラメータであるために、ノイズのほうが多くなってしまう。 ようするに、パラメータの多さは諸刃の剣なのである。
高次元なデータでは、結果と関係のない変数が互いに相関している可能性がある (3章でやった multicollinearity)。たとえば 50万種類の SNP と血圧の相関を 学習しようとして、17種類のSNPとの相関が発見された場合、これだけが唯一の 正しいモデルであるとは限らない (他にも正しいモデルが無数に存在するかもしれない)。 そのため、高次元なデータによって作られたモデルは、各データの特徴に 依存する可能性が高い (これはようするに過学習の別の言い方である)。
また、高次元なデータを使った場合、モデルの妥当性を二乗誤差や p-value や R2 で測定してはならない。p > n の状態では、これらは簡単に小さくなる。 モデルの妥当性はつねに訓練データとは別の、 独立したテストデータを使って評価するべきである。