An Introduction to Statistical Learning (4.1. 〜 4.4.)

権藤研輪講資料 2019/07/02
新山

4. Classification (分類)

はじめに

3章でやった変数 Y は量を表すものであった (quantitative)。
4章では変数 Y は種類 (カテゴリ) を表す (qualitative)。
このような変数は "categorical" とも呼ばれる。
与えられたものの種類を予測することを、分類 (classification) と呼ぶ。
分類器 (classifier) には多くの種類があるが、各カテゴリの確率を予測するような関数を仮定すると、これは回帰とも関連がある。
この章では代表的な 3つの分類器 (ロジスティック回帰, 線形判別解析, k-NN法) を扱う。

4.1. 分類とは

「分類」は、たとえば以下のような状況で使われる:

ある患者が救急車で運ばれてきたとして、各種検査結果から「心臓発作」「薬物中毒」「てんかん」のどれかを判定したい。
オンラインである品物が購入されようとしているとき、そのユーザの過去の購入履歴およびIPアドレスなどから、それが詐欺であるか否かを判定したい。
被験者の DNA 配列の中から、ある病気にかかりやすい配列とそうでない配列を特定したい。

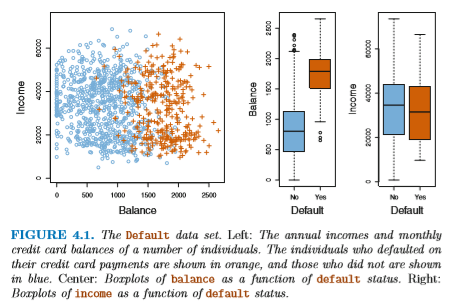
この章では、あるクレジットカード利用者の収入 (income) と利用額 (balance) から、その利用者が債務不履行 (default) を起こすかどうかを決定するタスクを例として利用する。ここでの分類の結果は "Yes (True)" あるいは "No (False)" のどちらかである。このような分類器を binary classifier という。 (これは 10,000件の利用者データからなるが、実際に債務不履行を起こす利用者は全体の 3% である。) ちなみに "債務不履行データ" では、利用額と不履行の可否に大きな相関があることがわかっている。

4.2. なぜ線形回帰ではダメなのか?

上記の例 a. を線形回帰でやろうとして、予測する値 y を以下のように決めるとする:

y == 1 : 心臓発作
y == 2 : 薬物中毒
y == 3 : てんかん

この割り当ては恣意的である。結果に「心臓発作」<「薬物中毒」<「てんかん」のような順序関係があるかどうかわからないし、「心臓発作」と「薬物中毒」の差 (?) が、「薬物中毒」と「てんかん」の差に等しい保証もない。

あるいは、3つのケースごとに独立した確率を線形回帰でモデルするという手もある:

y == 0 : 債務不履行の確率 0%
y == 1 : 債務不履行の確率 100%

この問題点は、直線で近似するため、確率がある時点で必ず 0 あるいは 1 を超えてしまうことと、 "債務不履行データ" をもとにした学習では確率がつねに低くなってしまうことである。

4.3. ロジスティック回帰 (Logistic Regression)

ここでは線形回帰のかわりに、確率をモデル化するのに適したロジスティック回帰 (logistic regression) を使う。

4.3.1. ロジスティック関数

確率を、以下のような関数でモデル化することを考える:

p(X)	=	exp(a + bX) /
		(1 + exp(a + bX))

この式を変換すると、以下のようになる:

p(X) / (1 - p(X)) = exp(a+bX)

問1. 上の変形を証明せよ。

ここで p / (1 - p) は、オッズ (odds) を表している。オッズは確率を別の方法で表したもので、競馬などの賭け事における払い戻し金を計算するのによく使われる。

たとえば p=0.5 の場合、オッズは 1 である。
確率が 0.5 以下の場合、オッズは 1 以下になり、
確率が 0.5 以上の場合、オッズは 1 以上になる。

(なお、日本の競馬で配当をあらわす「オッズ」は、実際にはここでいうオッズの逆数である。)

問2.

たとえば p=0.2 の場合、オッズはいくらか。競馬なら、配当は何倍か。
たとえば p=0.8 の場合、オッズはいくらか。競馬では、これはありえないが、それはなぜか。

4.3.2. Maximim Likelihood を使った推定

ロジスティック回帰の学習では、パラメータ a と b を推定する。このとき、

「positive」な例の確率が、なるべく p=1 に近くなるようにする。
「negative」な例の確率が、なるべく p=0 に近くなるようにする。

ようにすればよい。

これは以下のような Likelihood 関数を最大化するような a と b を求めることにより決まる (maximum likelihood 法):

L(a, b)	=	p(X_P0) × p(X_P1) × ... × p(X_Pn) ×
		(1 - p(X_N0)) × (1 - p(X_N1)) × ... × (1 - p(X_Nn))

4.3.3. ロジスティック回帰を使う

たとえば「債務不履行データ」の場合、ロジスティック回帰は、

p(債務不履行 == Yes | ある利用額)

の確率を推定することになる。ここで p > 0.5 なら「ヤバい」と判断すればよい。 (別のしきい値を使う手もありうる)

a:
b:

4.3.4. 複数の素性がある場合

ロジスティック回帰に入れる素性は複数あってもよい。この場合、確率を

p(X)	=	exp(a + bX) /
		(1 + exp(a + bX))

ではなく

p(X)	=	exp(a + bx₁ + cx₂ + ... ) /
		(1 + exp(a + bx₁ + cx₂ + ... ))

のようにモデル化する。

これを使って「債務不履行データ」を balance, income および student? の3つの素性でモデル化すると、素性 student? は債務不履行に対して負の相関があることがわかる。

いっぽう、student? だけの素性を使うと student? == Yes であるほど 債務不履行 == Yes しやすいという結果になる。これはなぜなのか?

実は balance が同じであれば student? == Yes のほうが 債務不履行 == Yes の確率が低い。ただし学生は一般に balance がより高いので、総合的に債務不履行 == Yes に寄与しているというわけだった。

4.3.5. カテゴリが3つ以上ある場合

Rを使えばできるけど、ここではやらない。

4.4. 線形判別解析 (Linear Discriminant Analysis)

注意: Linear Discriminant Analysis は通称 LDA と略されるが、自然言語処理の分野で LDA (Latent Dirichlet Allocation) という、まったく別の学習モデルもあるので混同に注意。

ロジスティック回帰は

P(Y==k | X==x)

をモデル化していた。 LDA では、正規分布していると仮定した変数 X と Y の相関をモデル化する。 LDA はカテゴリが 3つ以上あるときに威力を発揮する。

4.4.1. まず Bayes の定理を使う

まず密度関数 (density function)

f_k(X) = P(X | Y==k)

を考える。

Bayes の定理により

P(`Y==k` \| X)	=	P(`Y==k`) × f_k(X) /
		sum(P(`Y==i`) × f_i(X))

とモデル化できる。

問3. 上の式を導出せよ。

実際には f_k(X) の形を仮定しないと推定は難しい。LDA では f_k(X) をガウシアン関数

f_k(X)	=	exp(-1/(2×σ_k²) × (X - avg_k(X))²) /
		(sqrt(2×PI) × σ_k)

とする。

4.4.2. LDA (パラメータ数=1 の場合)

素性が1つしかない場合は簡単である。まず、簡単のため

σ₁ = σ₂ = ... = σ

と仮定し、これを上の Bayes の式に入れると

P(`Y==k` \| X)	=	P(`Y==k`) × exp(-1/(2×σ²) × (X - avg_k(X))²) /
		sum(P(`Y==i`) × exp(-1/(2×σ²) × (X - avg_i(X))²)

となる。ここで、

argmax_k P(Y==k | X)

となるような k を求める。

argmax_k (kが含まれている式) + (kが含まれていない式) = argmax_k (kが含まれている式)

であるので、最終的に

argmax_k (X × avg_k(X) / σ²) - (avg_k(X) × 2 × σ²) + log(P(Y==k))

となるような k を求めればよい。

問4. 上の式を証明せよ。

学習アルゴリズム

観測データをもとに avg_k(X) および σ² を求める。
P(Y==k) を求める。(数えるだけ)

問5. 式 (4.15) の間違いを発見せよ。

例として |k| = 2、P(Y==0) = P(Y==1) = 0.5 と仮定すると

Bayes 境界の位置 = (avg₀(X) + avg₁(X)) / 2

となる。

4.4.3. LDA (パラメータ数>1 の場合)

変数が 2つある場合、 σ のかわりに共分散行列 Cov(X₁, X₂) を使う。共分散行列は 2つの分布の幅および傾きを指定する。

ここでも、簡単のため Cov は各 k に対して同一であると仮定する。

実際にプログラムしてみた例 (自信なし):

機械学習のトレードオフ

"債務不履行" タスクの場合、分類の間違いには2種類のエラーが存在する。つまり「本来 Yes のはずのものを No と判定した」場合と、「本来 No のはずのものを Yes と判定した」場合である。これらを表 (行列) の形式で記したものを Confusion Matrix とよぶ。

問6. 上の confusion matrix 中の各数値の意味を、日本語で説明せよ。また、間違った分類結果の数は全部でいくつあるか。

じつは、この分類結果には実用上の問題がある。本来「債務不履行 == Yes であるものを No と判定してしまった」エラーが多いのである。これは 2種類のエラーの合計を最小化するようにしたためであるが、実際のクレジットカード会社にとっては一方のエラーのリスクのほうが、他方のエラーのリスクよりも大きい。そこで「債務不履行 == Yes」の確率を重視することにして、従来までは P(債務不履行 == Yes) > 0.5 であれば「Yes」と判定していたものを、 P(債務不履行 == Yes) > 0.2 であれば「Yes」と判定するようにする。すると、confusion matrix は以下のようになる:

こうすると、クレジットカード会社の恐れるエラーは減少する。が、全体的なエラーの合計は増えてしまう。

このような機械学習のトレードオフを表現するために、 ROC Curve というものがよく使われる。これは True Positive (正しく判定できた Yes の割合) と False Positive (間違って Yes と判定されたものの割合) をそれぞれ縦軸・横軸に表したもので、左上にいけばいくほどよく、曲線の右下部分の面積がその学習アルゴリズムの「能力」を表すと考える。

用語解説

実際の文献では、True Positive, False Positive などの割合はいろいろな用語で呼ばれている。以下に代表的なものを示す:

指標	使われる用語
\|間違った Yes 判定\| / \|すべてのYes物件\|	Type 1 error, 1-Specificity
\|正しい Yes 判定\| / \|すべてのYes物件\|	1-Type 2 error, Power, Sensitivity, Recall
\|正しい Yes 物件\| / \|Yes判定されたもの\|	Precision, 1-False dicovery proportion
\|正しい No 物件\| / \|No判定されたもの\|

4.4.4. Quadratic Discriminant Analysis (QDA)

これまでの例では、σ または Cov がすべての k に対して同一の場合を仮定していた。これが各 k ごとに異なると仮定すると、先の argmax の式は

argmax_k -(X - avg_k(X))² / (2 × σ_k²) - log(σ_k) / 2 + log(P(Y==k))

となり、x の2次項が残ってしまう。これが QDA である。

問7. 上の式を証明せよ。

QDA はより複雑な形状の分布を表現できるため柔軟性は高いが、同時に学習しなければならないパラメータが |k| p × (p+1) / 2 個になってしまう。少ないデータでは、これは過学習の危険性がある。 Bayes 境界が直線の場合、QDA よりも LDA のほうが適していることもある (下図)。

おさらい問題.

分類とは何か、説明せよ。
分類器とは何か、説明せよ。
なぜ分類を線形回帰として扱うとまずいのか、説明せよ。
ロジスティック回帰と LDA の違いは何か。
Binary classifier とは何か。
Confusion matrix とは何か。
ROC curve とは何か。
Type-1 error とは何か。
なぜ QDA よりも LDA のほうが過学習の危険性が少ないのか。

Yusuke Shinyama