第7回 ディープラーニング応用: 物体認識と奥行き推定

1. 画像認識の基礎 VGG
   • パディング (padding) とは
   • 演習7-1. VGG16 クラスを完成させる
   • バッチ正規化 (batch normalization) とは
   • 演習7-2. BatchNorm2d レイヤーを使う
   • Dropoutとは
2. 物体認識システム (YOLO) の実装
   • YOLO のニューラルネットワーク
   • YOLO の訓練
   • 演習7-3. YOLO の訓練を実行する
   • YOLO の後処理
   • 演習7-4. YOLO で実際に認識をおこなう
   • 自前の訓練データを作成する
   • さらに精度を上げるには
   • 発展課題. COCO データセットを使って学習
3. 奥行き推定システムの実装
   • ストライド (stride) とは
   • 奥行き推定における損失関数
   • 奥行き推定システムの訓練
   • 演習7-5. 奥行き推定システムの訓練を実行する
   • 演習7-6. 奥行き推定システムを利用する
4. まとめ

1. 画像認識の基礎 VGG

物体認識と奥行き推定の説明に入る前に、 まずニューラルネットワークを使った画像認識システム VGG を紹介する。 VGG は 2015年に発表された有名なディープニューラルネットワークであり、 その構造は画像を扱う多くのニューラルネットワークにも模倣されている。 これは与えられた画像を 1000種類のどれかに分類するものである:

VGG-16 は計16個のレイヤー (13個の畳み込みレイヤー + 3個の全結合レイヤー) からなるニューラルネットワークで、 ImageNet データセットに含まれる 1000種類の画像を 91% 程度の精度で認識できる。 (ImageNet データセットには約130万枚の訓練用画像が含まれているが、 著作権上の理由により、現在、一般には非公開となっている。)

• VGG が説明されている論文 "Very Deep Convolutional Networks for Large-Scale Image Recognition"

上の図にある Conv-3 (64) は 「3×3 のカーネルをもつ 64チャンネルの畳み込みレイヤー」をあらわす。 各畳み込みレイヤーおよび全接続レイヤーの後には ReLU 活性化関数が使われている。

VGG-16 の特徴は、以下の2点である:

1. レイヤーが深くなり、(Max Pooling により) 画像が小さくなるに従って、 チャンネル数は 64 → 128 → 256 → 512 と倍々で増えている。
   つまり、扱う情報の量は各レイヤーで変わらない。
2. Conv-3 (256) など同じチャンネル数の レイヤーを複数回重ねている。
   これにより、3×3 のカーネルを使っていても実際には 5×5 や 7×7 の領域の特徴を考慮することができる。

1.1. パディング (padding) とは

ここで、ディープな畳み込みニューラルネットワークで使われることの多い パディング (padding) という技術について説明する。 これまでは畳み込みレイヤーでカーネルを使うと、 以下のような問題があった:

• 入力画像に対して出力画像が (カーネルの大きさぶんだけ) 小さくなってしまう。
  たとえば 3×3 のカーネルを使った畳み込みレイヤーでは、 入力画像よりも出力画像が縦横 2ピクセルぶんだけ小さくなってしまう。 この調子で畳み込みレイヤーをいくつも重ねていくと、 画像がどんどん小さくなってしまい、それだけ考慮できる特徴量も減ってしまう。
• 画像の端にあるピクセルが十分に考慮されない。
  たとえば以下の図では、カーネルの中心が動ける範囲が赤線で示されている。 ここでは画像の左上隅にあるピクセルは1回しか カーネルが適用されない。これに対して中央付近のピクセルは9回 カーネルが適用され、ピクセルの位置によって扱いに差が生じてしまう。

この問題に対処するため、入力画像の周囲にピクセルをつめて 画像サイズを広げることにする。 3×3 のカーネルを使う場合は、画像の周囲に1ピクセル分の 架空のピクセルがあると想定すると、この中でカーネル中心が動ける範囲は もとの画像の大きさに一致する。

PyTorch では、nn.Conv2d レイヤーを作成するさいに nn.Conv2d(3, 64, 3, padding=1) などと指定するとパディングが使われる。 カーネルが 3×3 の場合、パディングを 1 にすると 出力画像のサイズは入力画像のサイズと正確に同じになる。

以上をふまえて VGG-16 を PyTorch のコードで記述すると、 以下のようになる。VGG16 クラスでは、 各畳み込みレイヤーと全接続レイヤーに conv1, fc14 などの番号をふっている。 Max pooling レイヤーは直前の畳み込みレイヤーと同じ番号にしてある:

import torch
import torch.nn as nn
import torch.nn.functional as F

##  VGG16
##
class VGG16(nn.Module):

    def __init__(self):
        nn.Module.__init__(self)
        # x: (N × 3 × 224 × 224)
        self.conv1 = nn.Conv2d(3, 64, 3, padding=1)
        self.conv2 = nn.Conv2d(64, 64, 3, padding=1)
        self.pool2 = nn.MaxPool2d(2)
        # x: (N × 64 × 112 × 112)
        self.conv3 = nn.Conv2d(64, 128, 3, padding=1)
        self.conv4 = nn.Conv2d(128, 128, 3, padding=1)
        self.pool4 = nn.MaxPool2d(2)
        # x: (N × 128 × 56 × 56)
        self.conv5 = nn.Conv2d(128, 256, 3, padding=1)
        self.conv6 = nn.Conv2d(256, 256, 3, padding=1)
        self.conv7 = nn.Conv2d(256, 256, 3, padding=1)
        self.pool7 = nn.MaxPool2d(2)
        # x: (N × 256 × 28 × 28)
        self.conv8 = nn.Conv2d(256, 512, 3, padding=1)
        self.conv9 = nn.Conv2d(512, 512, 3, padding=1)
        self.conv10 = nn.Conv2d(512, 512, 3, padding=1)
        self.pool10 = nn.MaxPool2d(2)
        # x: (N × 512 × 14 × 14)
        self.conv11 = nn.Conv2d(512, 512, 3, padding=1)
        self.conv12 = nn.Conv2d(512, 512, 3, padding=1)
        self.conv13 = nn.Conv2d(512, 512, 3, padding=1)
        self.pool13 = nn.MaxPool2d(2)
        # x: (N × 512 × 7 × 7)
        self.fc14 = nn.Linear(512*7*7, 4096)
        self.fc15 = nn.Linear(4096, 4096)
        self.fc16 = nn.Linear(4096, 1000)
        # x: (N × 1000)
        return

    def forward(self, x):
        # x: (N × 3 × 224 × 224)
        x = self.conv1(x)
        x = F.relu(x)
        x = self.conv2(x)
        x = F.relu(x)
        ...
        # x: (N × 1000)
        x = F.log_softmax(x, dim=1)
        return x

net = VGG16()
x = torch.rand((1,3,244,244))
y = net(x)

なお、実際に ImageNet の画像を使って訓練した VGG16 のモデルは torchvision モジュール として利用可能である。

1.2. バッチ正規化 (batch normalization) とは

さらにもうひとつ、VGG-16 発表時には知られていなかったが、 それ以降のディープラーニングでよく使われるようになった バッチ正規化 (batch normalization) と呼ばれるテクニックも 同時に紹介しておく。バッチ正規化は、各レイヤーにおける 入力の平均と分散が同一になるよう調整するものである。 バッチ正規化を使うと、各レイヤーへの入力が 同一の傾向をもつようになるため、学習の効率が高まり、 モデルの精度・学習速度ともに向上すると考えられている。 具体的には、各ミニバッチの平均と分散がそれぞれ β と γ になるよう調整する。 バッチ正規化の処理も微分可能であるので、 勾配降下法によって最適な β と γ を学習できる。

β と γ の値は各レイヤーの特徴量 (チャンネル) ごとに決定される。 バッチ正規化は、通常、活性化関数の直前に 「バッチ正規化レイヤー」をはさむことで実装する。 バッチ正規化レイヤーは現在のディープニューラルネットワークで 広く使われており、PyTorch でも標準で利用可能である:

• nn.BatchNorm1d(ノード数) … 全接続レイヤー (1次元) のためのバッチ正規化レイヤーを作成する。
• nn.BatchNorm2d(チャンネル数) … 畳み込みレイヤー (2次元) のためのバッチ正規化レイヤーを作成する。

class VGG16(nn.Module):

    def __init__(self):
        nn.Module.__init__(self)
        # x: (N × 3 × 224 × 224)
        self.conv1 = nn.Conv2d(3, 64, 3, padding=1)
        self.norm1 = nn.BatchNorm2d(64)
        self.conv2 = nn.Conv2d(64, 64, 3, padding=1)
        ...

    def forward(self, x):
        # x: (N × 3 × 224 × 224)
        x = self.conv1(x)
        x = self.norm1(x)
        x = F.relu(x)
        ...

1.3. ドロップアウト (dropout) とは

本講座では使わないが、かつてニューラルネットワークで よく使われていた ドロップアウト (dropout) という 正規化テクニックについても簡単に触れておく。 これは、訓練時にニューラルネットワーク中のノードをランダムに 「間引く (thinning)」ことにより学習精度を向上させるものである。 なぜノードを間引くと学習精度が上がるのか? これは、ニューラルネットワークのノードに見られる 「共適用 (co-adaptataion)」という現象によるものである。 共適用とは「あるレイヤー中の複数のノードが、 たまたま同じ特徴を学習してしまう」ことをいう。 レイヤー中のノードは並列に動作するため、 同一レイヤーの別のノードが何を学習しているかについては関知しない。 そのため、訓練の進み方によっては、お互いに知らないまま 2つのノードがほとんど同じことをしている、ということも起こりうる。 これはノードが無駄になっているということであり、 ニューラルネットワークの実際の学習能力が見かけのノード数よりも 低くなっているということである。

この現象を緩和するため、ドロップアウトでは 訓練中に (各ミニバッチごとに) あるレイヤーのノードを 一定の確率でランダムに「無効にする」。 無効にされたノードは値も出力せず、勾配も計算しない。 ただしこうすると各ノードの出力値の和が減少してしまうため、 間引いた分の定数をかけることによって全体のつじつまを合わせる、 といった処理をおこなう。

PyTorch では、ドロップアウトは nn.Drouout クラスを 使って簡単に実現できる:

• nn.Drouout(確率) … ある確率でノードを無効化する dropout レイヤーを作成する。

Dropout はニューラルネットワークの精度を上げるものの、 使い方が難しいという欠点がある。まず、dropoutレイヤーは どのレイヤーに追加してもよいというものではなく、 試行錯誤が必要である。また、意図的にノードを使用しないため 訓練に時間がかかる。いっぽうバッチ正規化は同様の効果が より効率的に得られるため、バッチ正規化が知られるようになった現在では ドロップアウトはあまり使われなくなってきている。

2. 物体認識システム (YOLO) の実装

YOLO (You Only Look Once) はディープラーニングを使った ポピュラーな物体認識アルゴリズムである。 これは画像をニューラルネットワークに一度通すと、 その中にどんな物体が、どの位置にあるかを判別できるようになっている。

• YOLO作者のページ。 オリジナルの論文や実装 (v1〜v3)、訓練後の重み・バイアスが公開されている。

(注意: 現在、YOLO には v1〜v5 までのバージョンがあり、 他にも条件を微妙に変えた様々なパターンが存在する。 本講座で取り上げるのは YOLO v1 をさらに単純化したバージョンであり、 認識性能は本物の YOLO ほどよくない。)

YOLO の基本的なアイデアは、 入力した画像 (224×224ピクセル) を 7×7 の升目 (セル) に分け、 おのおのに含まれている物体の種類と位置を推測するというものである。 まず簡単な問題として、7×7 の各セルに、あらかじめ定義した 20種類の物体のうちどれが写っているかを推測するタスクを考えてみよう。 入力はRGB画像とし、出力は各セルを 21要素の one-hot ベクトルで表現するとする:

MNIST や CIFAR-10 では画像全体にひとつのラベルを付与していたが、 ここでは物体 (あるいはその一部) が 7×7 の各セル内にどのように 分布しているかを予測させる (各セルの画像だけを見て物体を 判定しているわけではないことに注意)。 あとは、畳み込みニューラルネットワークを使って 入力から出力を推測させ、各セルの hot-oneベクトルを 交差エントロピー誤差で評価すればよい。 ここでセル c の出力を P(c)、 そのセルの正解 one-hotベクトルを P₀(c) とすると、 各セルごとの損失は、以下のようになる (H は交差エントロピー誤差を表す) :

最終的な損失関数 L は、各セルの損失を合計したものになる:

YOLOは上のタスクを拡張し、各セル内の物体の種類に加えて、 その座標および大きさ (=矩形) も推測させるようにしたものである。 YOLOの入力および出力は以下のようになっている:

ここで、確信度、矩形の相対位置、矩形の大きさの値は、すべて 0〜1 の範囲で 表現できるよう取り決めておく (相対位置と大きさはそれぞれ 2つの値で表すので、 合計 1+2+2 = 5つの値が必要になる)。 こうするとニューラルネットワークの出力であるシグモイド関数の値を利用できる。 ここでは物体をあらわす矩形の中央は該当するセルの中にあると仮定しているので、 セルの左上隅を (0, 0)、右下隅を (1, 1) として表現すれば相対位置を表せる。 また、物体の大きさは入力画像 (224×224) 全体が 1×1 となるように正規化すればよい:

これに物体の種類を表す20要素を加えると、各セルに対して 合計25個の要素 (チャンネル) が出力されることになる。 YOLO は、この各要素をやや変則的な方法で計算している。 最終レイヤーで各チャンネルごとに同じ活性化関数を使うのではなく、 確信度・相対位置・大きさを表す 5つのチャンネルにはシグモイド関数を、 物体の種類を表す 20チャンネルにはSoftmax関数を適用している:

(注意: 本物の YOLO では、各セルには1個ではなくk個の矩形が 所属できるようになっているが、ここでは簡単のため各セルは たかだか1個の矩形のみを含むとした)

YOLO では、各セルに物体の中心があるかどうかによって、 その損失を以下のように場合分けして計算している:

上の式で dx₀、dy₀、w₀、h₀ は それぞれ当該セルに含まれている正解の矩形の相対位置および大きさである。 確信度の正解 conf₀ はどうやって求めるのか? というと、 これは YOLO が予測した矩形と正解の 「重なり具合 (Intersection over Union, IOU)」を使っている (予測が完全に重なっている場合は 1 となり、まったく重なっていない場合は 0 となる)。 この式を見ると、矩形の相対位置・大きさに対しては標準的な二乗誤差を使い、 物体の種類に対しては交差エントロピー誤差を使っていることがわかる。 物体があるときに二乗誤差を 5倍し、ないときに 0.5倍しているのは (作者らによれば) 実際の画像では物体がないセルがほとんどであり、 こちらを優先させるためである。

2.1. YOLO のニューラルネットワーク

以下に YOLOの各レイヤー構造を示す (なお、これはオリジナルの YOLOv1 ではなく、 よりコンパクトな YOLOv2 をベースに簡単化したものである)。 VGG-16 と同様に、YOLO のネットワークは画像が縮小されるに従って チャンネル数が 2倍に増えるようになっている。ただし VGG-16 と異なり、 Conv-3 レイヤーの間に Conv-1 (1×1 のカーネルをもつ畳み込みレイヤー) が 挟まれた構造になっている。(著者らによると、このように中間の 畳み込みレイヤーを小さくすることによって、計算量を削減できるらしい。) なお、図中には示されていないが、各畳み込みレイヤーの直後に バッチ正規化レイヤーと活性化関数が挿入されている。

LeakyReLU活性化関数

YOLO のもうひとつの特徴として、活性化関数に 通常の ReLU ではなく LeakyReLU と呼ばれる 関数を使っていることがある。これは ReLU 関数を改良したもので、 通常の ReLU では x > 0 の勾配が完全にゼロになるところを、 LeakyReLU ではわずかに下向きの勾配 a をもつ。 従来の ReLU では x > 0 のときに勾配がゼロになり、 重みの更新ができなくなるが、LeakyReLU ではその間にもわずかな 勾配が残るため、重みの更新を行うことができる。

PyTorch では LeakyReLU は F.leaky_relu という関数で利用できる。 YOLO では、勾配として a = 0.1 を使っている:

x = F.leaky_relu(x, 0.1)  # a=0.1

2.2. YOLO の訓練

YOLO の訓練データには「PASCAL VOC データセット」というものを使う。 ここには約1万枚の画像と、そこに含まれている20種類の物体 (人間、自動車、椅子、犬、馬など) の矩形座標が記録されている。 なお後期バージョンの YOLOv3 では、より画像の数・種類ともに多い COCO データセットが使われている。

PASCAL VOC データセットの例

VOC データセットには、画像に加えて、 以下のようなXML形式の アノテーション (annotation) が付随している:

<annotation>
  <filename>000021.jpg</filename>
  <object>
    <name>dog</name>
    <bndbox><xmin>1</xmin><ymin>235</ymin><xmax>182</xmax><ymax>388</ymax></bndbox>
  </object>
  <object>
    <name>person</name>
    <bndbox><xmin>210</xmin><ymin>36</ymin><xmax>336</xmax><ymax>482</ymax></bndbox>
  </object>
  ...

これらのデータセットを使った、YOLO の訓練アルゴリズムは以下のようになる:

1. 画像を、ニューラルネットワークに通す。
2. 出力から損失を計算する:
   1. 各セルが予測する矩形の位置および大きさを計算する。
   2. セルに正解データの矩形 (の中心) が含まれている場合、 2つの矩形の IOU を計算し、上記 L_obj(c) を計算する。
   3. 含まれていない場合、予測された確信度から L_noobj(c) を計算する。
3. これらの損失を合計し、勾配を計算して重み・バイアスを更新する。

YOLO の訓練プロセスは、損失の計算方法が若干異なることを除けば、 他のほとんどニューラルネットワークと同じである。 ただし、実際には訓練データの XML を解析したり、 画像サイズをネットワークの入力 (224×224) に合わせて調整したり、 それに合わせて各セルごとの正解値を求める処理が結構複雑である。 このように、実際の機械学習のタスクにおいては、ニューラルネットワークの 学習そのものよりも、データの準備や結果の後処理などのプログラミングに 手間がかかることが多い。

以下に、YOLO を実際に実装してみたものを紹介する。 ここではモデルを簡単にするため、2種類 (人・自動車) の物体のみを認識するように なっている。

2.3. YOLO の後処理

さて、YOLO では各物体の中心にもっとも近いセルだけが 矩形の情報をもつことになっているが、実際にはすべての セルに (確信度は低いものの) 矩形の情報が出力される。 これらの矩形をすべて有効とすると、ひとつの物体に対して 大量の矩形が出力されてしまう。そこで YOLO は出力に対して Non-Max Suppression (NMS) と呼ばれる後処理をおこなっている。 (NMS は YOLO に限らず、物体検出で一般的に使われている処理である。)

NMS の原理は単純である。これは確信度のもっとも高い矩形をとり出し、 それとある一定以上の比率で重なっている矩形をすべて削除していけばよい。

今回は後処理として、NMS の改良版である Soft-NMS という方法を使っている。 これは重なり合った各矩形を即削除するのではなく「確信度を減らす」 ことにより徐々に順位を下げていく方法である。 Soft-NMS の具体的なアルゴリズムは以下のようになっている:

1. 現在、もっとも大きな確信度をもつ矩形を出力する。
2. それと重なる各矩形の比率 (IOU) を計算し、それらの確信度を exp(-C · IOU2) 倍する。
3. 一定のしきい値以上の矩形がなくなるまで 1. 〜 2. を繰り返す。

この結果、得られた矩形を表示すれば物体認識は完了である。

• Soft-NMS が説明されている論文 "Soft-NMS - Improving Object Detection With One Line of Code"

mAP (mean Average Precision) とは

ここで、mAP (mean Average Precision) という概念について説明しておく。 mAP は物体認識や情報検索の評価に使われる指標のひとつである。 実際には、こういったタスクの評価は簡単ではない。 すべての物体が (種類・矩形とも) 完璧に認識できた場合は単純なのだが、 以下のようなケースに対して適切なペナルティを与えたいからである:

• 認識されるべき物体を認識しなかった場合
• 同一の物体を、2つの異なる物体として認識した場合

mAP は個々の物体に対する認識結果の AP (Average Precision) を平均したものである。 各AP は以下のようにして計算する:

1. ある種類の物体において、認識された矩形を、確信度の高い順に並べる。
2. 上位 n個の認識結果に対して、そのうちのいくつが 正解データに IOU ≥ 0.5 以上で一致しているかを数える。 (ただし、一度正解とみなした物体は二度数えない。)
3. n を 1 から徐々に増やしていき、そのときの出力に含まれる 正解の比率 (適合率) を、正解データ全体に対する比率 (再現率) によって積分する。
   たとえば、4個の物体 (正解) に対して5個の矩形が出力された場合:
   • n = 1 の結果: [○] (適合率 1/1、再現率 1/4) … 1/1 × 1/4
   • n = 2 の結果: [○, ×] (適合率 1/2、再現率 1/4)
   • n = 3 の結果: [○, ×, ○] (適合率 2/3、再現率 2/4) … 2/3 × 1/4
   • n = 4 の結果: [○, ×, ○, ○] (適合率 3/4、再現率 3/4) … 3/4 × 1/4
   • n = 5 の結果: [○, ×, ○, ○, ×] (適合率 3/5、再現率 3/4)
   この画像の AP は (1/1 + 2/3 + 3/4) × (1/4) ≒ 0.60 となる。
4. すべての種類の物体に対して AP を計算し、その平均を取って mAP とする。

2.4. 自前の訓練データを作成する

YOLO に新しい種類の物体を認識させるためには、訓練データとなる PASCAL VOCデータセットのようなもの (アノテーション) を自分で作成する必要がある。 このためのソフトウェアを 画像アノテーションツール (image annotation tools) という。画像アノテーションツールは商用・フリーのものを含めて 多くの種類が存在するが、ここでは VGG の開発チームが製作した、 VGG Image Annotator (VIA) というツールを使用する。これはブラウザベースで動くため、 追加のインストールは必要ない。 VIA にはバージョン 2系列と バージョン 3系列があるが、 今回は バージョン2 を利用する (こちらのほうが使い勝手がよいため)。

1. via-2.0.11.zip をダウンロード・展開し、 ブラウザで via.html ファイルを開く。
2. 画面左側にある「Project」パネルから、 Add Files ボタンをクリックし、 アノテーションを追加したい画像を選択する。
   
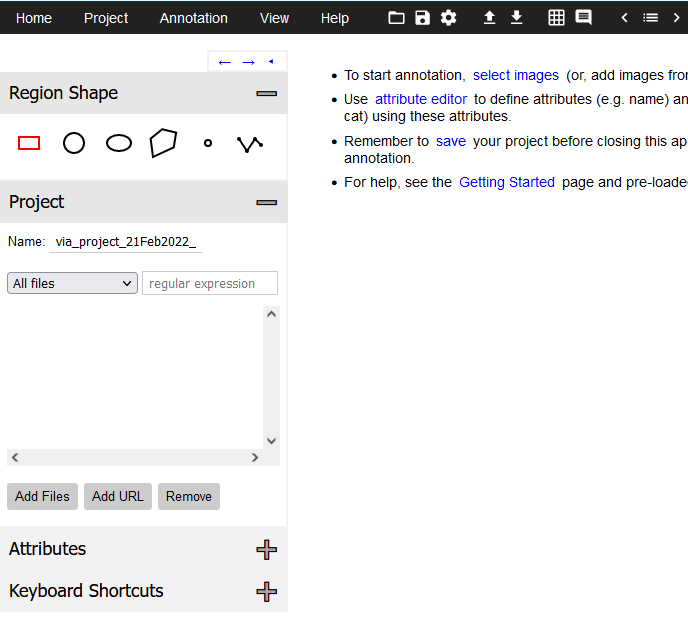
3. 画面左側にある「Attributes」パネルを開き、 "attribute name" 欄に "name" と入力して + ボタンを押す。 ここでは属性の型 (Type) は "text" としているが、 いちいち種類を手入力するのが面倒な場合は、 これを "dropdown" に切り替え、選択肢を入力してもよい。 (この作業が必要なのは一度だけである。)
   
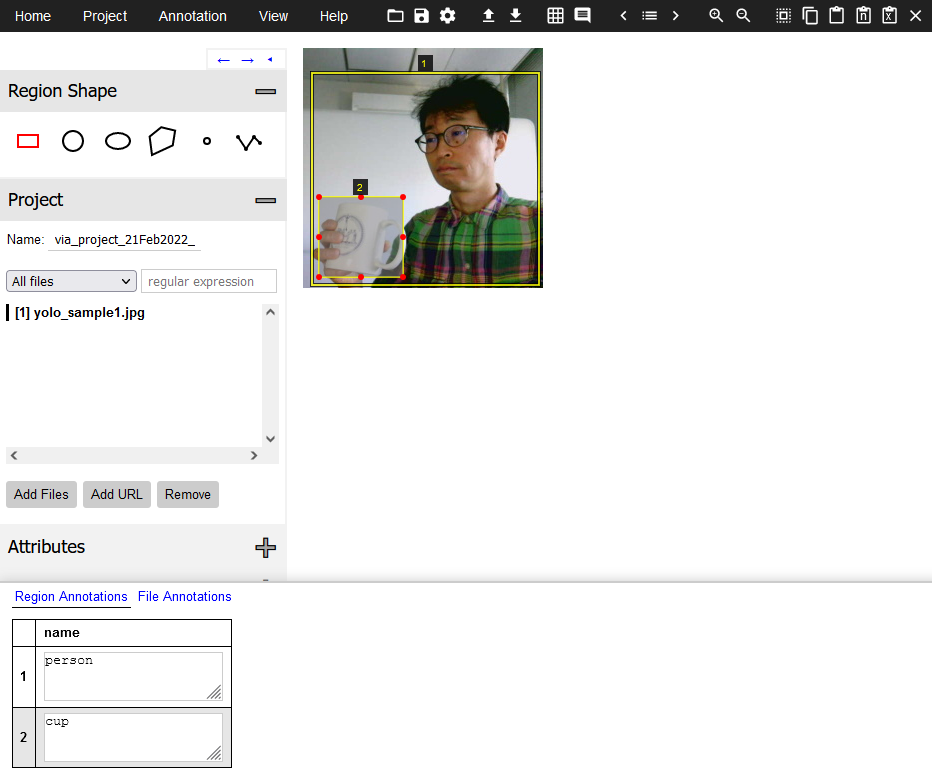
4. 画像中をドラッグし、矩形領域を作成して name欄にそれぞれの 物体の種類を入力する。なお、画面下部の属性パネルは Space キーでオン・オフ可能である。
   
5. 画面上部の「Annotation」メニューから Export Annotations (as json) を選択する。 ブラウザからjsonファイルがダウンロードできる状態になるので、 これをファイルに保存する。
6. 途中経過を保存・再開する場合は、 画面上部の「Project」メニューから Save あるいは Load を選択する。

完成した JSON形式のファイルを PASCAL VOCと同等の XML形式に変換する via2voc.py というツールを用意した。 これは以下のようにして利用する:

C:\> python via2voc.py -O. output_json.json
loading: output_json.json
saved: ./yolo_sample1.xml
...

2.5. さらに精度を上げるには

今回実装した YOLO の精度は、論文に載っている「本物」バージョンの YOLO よりも低い。 その最大の理由は、使っている訓練データの不足である。 本物の YOLO では、検出精度を高めるために以下のような方法を使っている:

データ拡張 (data augmentation)

画像認識のタスクでは、訓練データをいわば「水増し」するために データ拡張 (data augmentation) というテクニックを使うことが多い。 これは、もともとの画像にランダムな変換をほどこして訓練データに混ぜるもので、 必要な場合は正解の矩形データもそれに合わせて変換する (切り取り・左右反転など)。 データ拡張をおこなうことによって、訓練データを自動的に増やすことができる。 これはモデルが単純な特徴 (画像全体の明るさや、隣り合ったピクセルの色など) だけで 物体を判定するのを防ぎ、結果として精度が向上すると考えられている。

明るさを変える	色調を変える	ノイズ付加	切り取り	左右反転	画像の混合

事前学習 (pretraining)

訓練データの不足を補うのに使われるもうひとつの方法が 事前学習 (pretraining) である。これは「ニューラルネットワークの一部 (または全部) を、 あらかじめ (より訓練データが多い) 別のタスク用に訓練しておき、 その後本来のタスク用に訓練しなおす」というものである。

たとえば YOLO の論文では、最初の 13層の畳み込みレイヤーを まず ImageNet 用に訓練している。ImageNet は画像に含まれる物体が 1000種類のどれかを判定する単純なタスクであるが、PASCAL VOC に比べて 画像の数が数百倍多い。YOLO では、まず 13層の畳み込みレイヤーに 1000ノードの全接続層と Softmax活性化関数をつけたものを作り、 これを ImageNet の判定用に学習させる。つぎに 13層の畳み込みレイヤーの 重み・バイアスを残したままで畳み込みレイヤーを つけたし、今度は PASCAL VOC を使って YOLO 用に学習させる。 こうすることによって、ImageNet で学習した知識を YOLO にも 転用できると期待されている。

事前学習は、より一般的な手法である 転移学習 (transfer learning) と呼ばれるテクニックの一種とみなすことができる。 事前学習は、画像認識の分野では頻繁に利用されている。 これは「最初のほうのレイヤーが学習する特徴量は、 多くの画像認識関連のタスクで共通に利用可能であろう」という 仮説によるものである。多くの論文によれば、事前学習によって実際に 認識精度が向上することが報告されている。

PyTorchによる他のオープンソース実装

• PyTorch を使った YOLO v3 の実装: PyTorch-YOLOv3
• 画像データに関するデータ拡張をおこなう Python ライブラリ: imgaug

3. 奥行き推定システムの実装

次に、2次元画像のみから (距離センサなどを使わずに) 畳み込みニューラルネットワークを使って 奥行きを推定するシステムを紹介する。 これは以下の論文で説明されているものである:

• 奥行き推定システムの作者のページ。 オリジナルの論文や実装、訓練後の重み・バイアスが公開されている。

この研究では NYU Depth データセット というものを使っている。 ここには RGB画像と、赤外線センサによって得られた奥行き情報が ピクセルごとに関連づけられており、 ニューラルネットワークは画像と (1/4 ほど粗くした) 奥行き値との 対応関係を学習させている。

NYU Depth データセットの例

• 入力: 304×228ピクセルからなる RGB画像
• 出力: 各ピクセルの奥行きをあらわす、74×55 の行列 (画像の約1/4)

ここで使われているニューラルネットワークも VGG-16 を参考に作られている。 このシステムで特徴的なのは、最終的な結果を得るのに 2つのニューラルネットワークを 使っていることである。最初の「粗い (coarse)」ネットワークでは 入力画像からおおざっぱな奥行き情報のみを取得し、 次の「細かい (fine)」ネットワークでもう一度もとの画像を参考に 情報を洗練するというプロセスをとっている。 ここでも図中に示されていないが、各畳み込みレイヤーの直後には バッチ正規化レイヤーと ReLU 活性化関数が挿入されている。

奥行き推定システムの訓練は、2段階に分けて行われる。 まず訓練データを使って Coarse ネットワークだけを訓練し、 重み・バイアスを固定する。つぎに同じ画像を使って Fine ネットワークを訓練するが、このとき Coarseネットワークを 推論として使い、その結果を途中の (63×74×55) のチャンネルに 追加し 64チャンネルとしている。

3.1. ストライド (stride) とは

上の図中にある「Conv-11, /4」「Conv-9, /2」という 畳み込みレイヤーは、それぞれ 「11×11のカーネルを使った、ストライド4の畳み込みレイヤー」 「9×9のカーネルを使った、ストライド2の畳み込みレイヤー」 を表している。ストライド (stride) とは、 カーネルが画像上を動くときの刻み幅のことである。 通常、カーネルのストライドは 1 だが、この例のように 2 や 4 のケースも存在する。ストライドが 2 の場合、カーネルが適用される ピクセルは下図の斜線部分のように「ひとつ飛ばし」になり、畳み込みの結果は 元画像の 1/2 に縮小されたものになる。これは max pooling とほぼ 同じ効果をもたらすが、ストライドを増やすか max pooling を使うか、 あるいは本手法のように両方使ったほうがよいのかは、はっきりとは決まっていない。

PyTorch では、nn.Conv2d レイヤーを作成するさいに nn.Conv2d(3, 96, 11, stride=4) などと指定するとストライドが指定できる。

3.2. 奥行き推定における損失関数

奥行き推定システムでは、Coarse・Fine ネットワークのどちらも、 最終層で活性化関数を使わず、各ピクセルの推定距離 y を直接メートル単位で 返すようになっている (厳密には、距離の対数 log(y) を返す)。 このとき、正解に対する損失関数として、通常の平均二乗誤差ではなく 「スケール不変平均二乗誤差 (Scale-Invariant Mean Squared Error)」 というものを使っている。 これは、出力の絶対値だけでなく、その変動もできるだけ正解に 近づけるためである。通常の平均二乗誤差だけを使った場合、 値の大きさだけが重視されるため、「大きな値」と「小さな値」の差異は 検出できるものの、「大きな値」どうしの細かな差異は 相対的に小さくなってしまう:

奥行き推定システムでは 2つの誤差の平均をとって、 以下のような損失関数を使っている:

スケール不変平均二乗誤差 L_SIMSE は、以下のようにして求められる:

3.3. 奥行き推定システムの訓練

以下に PyTorch を使った奥行き推定システムの実行方法を紹介する。 奥行き推定システムの訓練は、2段階に分けて行われる。 まず Coarse ネットワークを訓練し、つぎに同じ訓練データを使って Fine ネットワークを訓練する。このとき Coarseネットワークを 推論として使っている。 訓練データとして使う NYU Depth データセットには 1,449枚の画像が含まれているが、これだけだと少ないため 訓練時には簡単なデータ拡張 (左右反転・色調補正) をおこなうようにしている。

4. まとめ

• VGG-16 は画像認識をおこなう有名なディープニューラルネットワークである。
• パディングとは畳み込みレイヤーの画像の周囲に余分なピクセルを追加するテクニックである。
• バッチ正規化は、各レイヤーにおける入力の平均・分散を調整する仕組みであり、モデルの精度・学習効率ともに向上する。
• 物体認識システム YOLO は、画像を 7×7のセルに分割し、それぞれに含まれる物体の種類および矩形を推測する。
• 奥行き推定システムは、まず画像のおおまかな奥行きを推定し、つぎにそれを洗練するという2段階のニューラルネットワークを使って実装されている。
• データ拡張とは、画像データにさまざまな変換を施すことによって、訓練データを自動で増やすテクニックである。
• 画像処理のタスクでは、ImageNet などの大量の画像を使った事前学習が本番のタスクの前に行われることが多い。

この作品は、クリエイティブ・コモンズ 表示 - 継承 4.0 国際 ライセンスの下に提供されています。